 (卓上の音楽) |
音楽の原点を探る |
画像加工広場 老夫婦の旅記録 |
１．背 景普段の会話で当たり前のように飛び交う言葉の中にも解らないことが沢山ある。音階ができた背景は？、美しい音色とは？、音色を決める倍音の正体は？、ハーモニーの正体は？、 楽しい／悲しい響きとは？、楽曲の仕組みは？、等々、関心ごとは沢山あり、これらを自然現象の中から学ぼうとした。 人は、本能のままに音楽との繋がりを築いてきた。ならば音楽は人為的に考えられた約束事ではなく、自然現象の中から生まれた事象だろうと推察できる。 たとえば、５度の調和、倍音列の響き、差音のハーモニー、規則的リズムの中の不規則な揺らぎ、など、音楽の原点が自然法則の中にある。 その自然法則というのは実に合理的に出来ており、足し算より引き算の美意識の方が合理性に叶う。 そう考えると、音楽ありきで総花的に学ぶより、身近な自然現象の中から音楽を学んだ方が、理解が深まることを実感した。 そこで、これまで断片的に得た音楽の知識を、復習と整理を兼ねて備忘録のつもりで纏めてみました。
２．自然現象の中から音楽を学ぶと理解しやすい ・・・ 音楽と人の本能
３．和む音には、不規則な揺らぎがある ・・・ Simple is Best
４．鍛冶屋の鉄打つ音から音楽の存在を予想 ・・・ ピタゴラス音律の誕生
５．ピタゴラス音律 ・・・ ミ-ファ、シ-ド間が半音なのは？
６．平均音律と純正音律 ・・・ それぞれの歩みと特徴
７．各音律の特徴、音程の話／音の調和とは
８．協和音・不協和音について
９．自然に発生する音はすべて正弦波の組み合わせ ・・・ 倍音の誕生
10．ハーモニック（高調波・倍音・調和）と 倍音列
11．基音が音程を決め、倍音が音色を決める
12．和音・差音・うなり音・ハーモニー ・・・ 差音の謎：綺麗な音と嫌な音
13．共振・共鳴・同調群軽折軸(ぐんけいせつじく)という言葉があります。 「小さな力も数多く集まれば大きな力になる」というたとえで、極めて軽いものでも多く積めば重くなり、それを載せた車の軸が折れてしまう意味です。 微細なエネルギーでも互いに助け合えば大きなエネルギーになる。それが共振・共鳴だと思います。 音波は空気の振動、電波は電磁界の振動、地震波は大地の振動であり、 あらゆる物は固有振動数をもっていて、外部からの振動周期に一致すると共振・共鳴によってエネルギーが伝わり、更に大きく振動する。 共振現象には厄介な問題もあるが、楽器や機械、電気・電子回路、とりわけ電波を利用する無線機器などできわめて重要な役割を果たしています。 物体の固有振動については3章で見たように、今から2,500年も前に、ギリシャの哲学者で数学者でもあったピタゴラスが予言していました。 共振現象の厄介な問題と言うのは、1940年、アメリカ・ワシントン州で開通してわずか4ヶ月後の吊橋が強風を受け、捻れて壊れてしまったそうです。 この吊橋は風速60m/sまで耐えられるよう設計されていたそうですが、わずか風速19m/sで落下してしまうという共振の怖さを知る事故でした。 風速19m/sだから、最初はゆっくり揺れていたのでしょうが、次第に強風の周期に同調して捻じれ振動が増幅し、 吊橋の強度がついには持ちこたえらず落下してしまったそうです。 大勢の人が列を成して吊橋を渡る際も、人の歩調が吊橋の固有振動に一致すると大揺れになり危険です。 実際に過去にフランスで事故があり、「吊橋の上で歩調をとるべからず」という立札を置いたそうです。 地震の場合も同様です。建物が地震に同調すると倒壊の恐れがあるので建物の偏心率(重心と剛心のずれ)を抑えるよう設計されます。 楽器は、この共振・共鳴という増幅現象を利用して音を遠くへ届けます。 共鳴箱という物があります。一言で言えば、「音を増幅させる箱」のことです。 ■その原理は！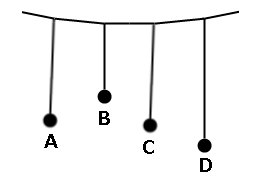 
図のように様々な長さの振り子Ａ～Ｄを吊るし、振り子Ａを揺らすと、それと同じ長さの振り子Ｃも徐々に揺れ始め、違う長さの振り子ＢとＤは静止しています。振り子は糸の長さだけで決まる固有振動数を持っており、振り子ＡとＣは固有振動数が同じだから、ＣはＡによって共振運動をするのです。 このように、個々の物体が持つ固有振動数と同じ振動数の揺れを外から加えると物体が振動を始める現象を共振、音の共振現象を共鳴と言います。 言い換えれば、Ｃはもともと自分固有の振動を持っており、そこへＣと同じ振動を外から与えてやるから共振してＣも動き出すということです。 ブランコも同じで、ひもの長さによって固有振動数が決まっており、体重が軽い人・重い人、どちらが乗っても揺れる周期は変わりません（理屈上）。 一方、振り子Ａを大きく揺らすと、同じ長さのＣだけでなく、ＢもＤも揺れはじめるかもしれません。 これは、ＢやＤ独自の固有振動に、Ａの強い振動を強引に押しつけ、ＢやＤのもつ固有振動を変えてしまうこともありますが、これは共振ではなく、ＢやＤがＡに同調すると言うことです。 つまり、共振・共鳴は受動的で、同調は能動的に発生する現象です。 言い換えれば、お互いに干渉し合う現象が共振・共鳴で、 どちらか片方が一方的に強制力で相手を動かす現象が同調ということです。先ほどの地震の話はこの例です。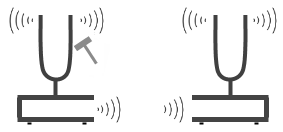 
もう一つの例として、同じ固有振動数を持つ共鳴箱付き音叉を２つ用意して、片方を鳴らすと、もう片方も鳴り始める。
叩かれた音叉が下の共鳴箱を揺らし、空気を伝わって隣の共鳴箱を揺らし、その上の音叉を揺らします。
これは、２つの共鳴箱が同じ固有振動数を持っているからです。固有振動数が違う音叉同士では共鳴は起こりません。 音叉を単体で叩けば発生する音は小さいが、共鳴箱に繋がると大きい音になります。 これは、音叉の振動で共鳴箱が共振して、音が増幅されるから大きく響くのです。 そして隣の共鳴箱にその振動を伝えるのです。 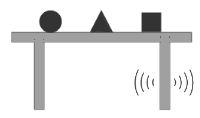 次の例は、机の上に、100Hzの固有振動を持つ物体●、110Hzの固有振動を持つ物体▲、120Hzの固有振動を持つ物体■を置き、 机の脚に110Hzの振動を与えると、物体▲だけが振動を始めるという、手品で使えそうな実験例です。 物体●が不安定で直ぐ動きそうだが、共振するのは物体▲です。 楽器は、この共振・共鳴現象を利用して作られます。 先ほど共鳴箱は音を増幅するもの、と言いましたが、それだけではなく、共鳴する音の周波数を選択するという役割もあります。その例は、 
笛系は皆同じでしょうが、たとえば、分かりやすい例として、篠笛では、音種ごとにその周波数に合った位置に孔をあけて音を共鳴させます。
孔の位置は、4章で見たピタゴラスの実験からも推測できます。
音階の変化は、複数の孔の開閉の組み合わせで共鳴する音を変えます。
たとえば、ド音は孔を6個塞いで1個開けます。
オクターブ上げた高音域の音を出すときは吹口へ空気を細く速く吹き込むことによって共鳴音域を高くします。
更に、その孔の大きさでも共鳴させる周波数が変わり、孔が大きいと共鳴する周波数が特定でき、孔が小さくなると少しずれた周波数になる。
つまり、孔を塞ぐ量によって共鳴する周波数を半音くらいは変えることができます。弦楽器の場合、音の共振・共鳴がどうなっているのか、よく解らなかったので少し調べてみました。 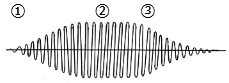 バイオリンを例にすると、弓に圧力をかけて弦を擦ったとき、その摩擦力で発生するエネルギーを貰って弦が振動を続けます。 右図は、バイオリンの弓で弦を弾くときの過程を波形で表したものです。①弓に圧力を加えて弾き始める、②弓で弾き続ける、③弓を止めて弦から離す、の様子を示しています。 弾き始めるたとき、①音の振幅が次第に大きくなっていく、②同じ圧力で弾き続け、弓を止めて弦から離すと③音の振幅は次第に減衰しいきます。  この弦の振動は、表板の上に立てられた「駒」に伝えられ、その振動がさらに表板に伝わります。 響胴を構成する表板と裏板の間には、両方を繋ぐ「魂柱(こんちゅう)」とう細木の棒が響胴内に立てられており、これが表板の振動を裏板に伝えます。 魂の柱と言うくらいですから重要なパーツだろうと想像できます。 表板・裏板に伝わった振動が胴内でお互いに共振・共鳴し合って音を増幅し、 サウンドホール」と呼ばれる「ｆ字型の孔」を通して大きな音を出しているようです。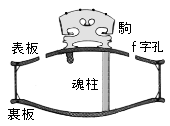 
このｆ字孔は音のエネルギーを放出する出口なので重要そうですが、なぜ「ｆ字」なのかは分りません、デザイン的理由との話もあるようです。
何れにせよ、あの弓で弦を弾く小さな音が、響胴の中であれだけ迫力のある音に増幅できるのが不思議です。一方、弦楽器では、倍音を多く含むよう設計（11章｢倍音の多い音の例｣）されているようですが、なぜひょうたん型か、くぼみが音響的に効果があるのか調べてみたが分りません。 ここでもデザイン的理由の説が多いです。 17～18世紀に活躍した名工、ストラディバリが作ったもで、存在が確認されている数がおよそ６００本あるそうで、 今では１０億円近い値で取引されることもあるそうです。音色の違いがよく分らないけど。 音楽では、この共鳴音をどう創り出すかが大切で、楽器によって決まる部分と、演奏の仕方によって決まる部分があります。 後者については、11章の「音色は倍音によって決まる」で触れたように、倍音を意識したり、曲想の理解して演奏するだけでも変化があると考えられます。 
14．調の成り立ち：テトラ・コード（TetraChord） ・・・ 短音階の謎
15．五度圏図・調号と臨時記号 |
Copyright ©2019 - Smo. All rights reserved. Last Updated 09/18/2019.