 (���̉��y) |
�@���y�̌��_��T�� |
�摜���H�L�� �V�v�w�̗��L�^ |
 �P�D�w �i
�P�D�w �i�@���i�̉�b�œ�����O�̂悤�ɔ�ь������t�̒��ɂ�����Ȃ����Ƃ���R����B���K���ł����w�i�́H�A���������F�Ƃ́H�A���F�����߂�{���̐��̂́H�A�n�[���j�[�̐��̂́H�A �y�����^�߂��������Ƃ́H�A�y�Ȃ̎d�g�݂́H�A���X�A�S���Ƃ͑�R����A���������R���ۂ̒�����w�ڂ��Ƃ����B �@�l�́A�{�\�̂܂܂ɉ��y�Ƃ̌q�����z���Ă����B�Ȃ�Ή��y�͐l�דI�ɍl����ꂽ���ł͂Ȃ��A���R���ۂ̒����琶�܂ꂽ���ۂ��낤�Ɛ��@�ł���B ���Ƃ��A�T�x�̒��a�A�{����̋����A�����̃n�[���j�[�A�K���I���Y���̒��̕s�K���ȗh�炬�A�ȂǁA���y�̌��_�����R�@���̒��ɂ���B ���̎��R�@���Ƃ����͎̂��ɍ����I�ɏo���Ă���A�����Z�������Z�̔��ӎ��̕����������Ɋ����B �����l����ƁA���y���肫�ő��ԓI�Ɋw�Ԃ��A�g�߂Ȏ��R���ۂ̒����特�y���w�����A�������[�܂邱�Ƃ����������B �����ŁA����܂Œf�ГI�ɓ������y�̒m�����A���K�Ɛ��������˂Ĕ��Y�^�̂���œZ�߂Ă݂܂����B  �Q�D���R���ۂ̒����特�y���w�ԂƗ������₷���@�@�@�@�@�@�@�E�E�E�@���y�Ɛl�̖{�\
�Q�D���R���ۂ̒����特�y���w�ԂƗ������₷���@�@�@�@�@�@�@�E�E�E�@���y�Ɛl�̖{�\ �R�D�a�މ��ɂ́A�s�K���ȗh�炬�������@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@Simple is Best
�R�D�a�މ��ɂ́A�s�K���ȗh�炬�������@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@Simple is Best �S�D�b�艮�̓S�ł����特�y�̑��݂�\�z �@�@�@�@�@�@ �E�E�E�@�s�^�S���X�����̒a��
�S�D�b�艮�̓S�ł����特�y�̑��݂�\�z �@�@�@�@�@�@ �E�E�E�@�s�^�S���X�����̒a�� �T�D�s�^�S���X����
�T�D�s�^�S���X�����@�O�͂ł́A�Ȃ��u�I�N�^�[�u�v�Ƃ����P�ʂȂ̂��A�����P�I�N�^�[�u��12��(=3X4)�̉��̂��ǂ̂悤�ɂ��Ăł����̂��A 4��(a)�̗��v��Ǝ��̂悤�ɂȂ�܂��B �b�͊ȒP�ŁA����w���ɒ��a����x����T�����Ƃł���A�x�����������玟�ɂx���ɒ��a����y����T���A�Ƃ�����ɒ��a���鉹�����X�T���Ă����悢�B �͂����ŒT���Ă��悢���A���R���悭�ώ@���Ă݂�ƁA���a���鉹�́A���g����(������)��1:2�A2:3�A3:4�̂Ƃ��ł��邱�Ƃ��O�͂ł��łɉ����Ă��܂��B 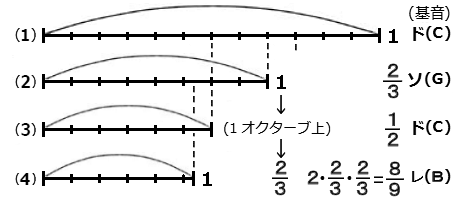 ���̌��ۂ���ɁA�s�^�S���X�͈ȉ��̂悤�ɂ��ĂP�I�N�^�[�u12���K���o�����B ���̕��@�͑O�q�S���̃g���C�A���O���̗���J��Ԃ��悤�Șb�ɂȂ�܂����A (1)�����P�̈�{�̌���p�ӂ��ĉ���炵�Ă݂�B (2)���̌��̒������R���̂Q�̌���p�ӂ��ĉ���炵�Ă݂��(1)��荂�������o��B (1)��(2)�̌����ɖ炷�ƁA���̂Q�̉��͂悭���a����̂ŁA�̂̐l�͂��̎����𗘗p���͂��߂܂����B ���ꂪ�a���̒a���ł��B (1)�̌���U�������ăh���������Ƃ��āA(2)�̌���U��������ƁA���̐U������(1)��3/2��1.5�{�A�܂�h����1.5�{�̓\���ɂȂ�܂��B ���̗��R�͂��̌�ɏo�Ă��܂��B�@�@�@�i���g�����P�^���̒����j ����(2)�̌����P�Ƃ��āA����2/3�{�̌�(4)������ĉ����Ă݂��(2)���X�ɍ����������Ă���A(2)��(4)�͂悭���a����B �����āA(2)���\�����Ƃ����(4)�̉��̓\����3/2��1.5�{�U�������������B �X�ɁA(4)�͊�h(1)��2X(1/2)X(3/2)X(3/2)=2X(9/8)=2X1.125�{�A�܂�2.0�{�͂P�I�N�^�[�u��̃h���ɂȂ�̂ŁA���̃h���ׂ̗̃����́A1X(9/8)=1.125�{�ɂȂ�A�Ƃ������Ƃł��B ����(4)��2/3�{�̌������A��L�Ɠ������Ƃ��J��Ԃ��ƁA���̌��̓�����1.5�{�U�������������ɂȂ�B �X��(4)�̌����P�Ƃ��āA����2/3�{�̌�(4)�����]�X�A������J��Ԃ��Ă����ƍŌ��12�Ԗڂ̉�(�t�@)�����܂�܂��B�@ �������A(1)�̌��̒������P�̂Ƃ��h���������Ƃ��A���̌��̒�����(2/3)��(8/9)�ɂȂ�ƁA�Ȃ��\��ɂȂ�̂��A���̎��_�ł͂܂��������܂���B ����́A���̎菇��ǂ��āu�h���~�t�@�\���V�h�v�̉��K������Ă݂��Ƃ�����܂��B �@(��) ��L�̌��ۂ���ɁA�s�^�S���X�����������Ă݂� �@��{�́A���̒�������2:1(���S8�x)�ɂ���ƁA���͂P�I�N�^�[�u�����Ȃ�A�݂��̉����悭���a���邱�Ƃ͉���܂��B ����Ɍ��̒�����3:2(���S5�x)�A4:3(���S4�x)�ɂ����Ƃ����݂��ɒ��a���邱�Ƃ𗝉�������ŁA���}�̂悤�ɉ��K�������Ă݂܂����B �@�s�^�S���X�́A���ۂɂ������̎��g����2:3�̐ςݏd�˂ʼn��K�����Ƃ����̂ŁA�����ł����̒�����(3:2)�����𗘗p���ăI�N�^�[�u���̉��K�������������܂��B ���A���g����{�ɂ���ƂP�I�N�^�[�u�����������ɂȂ�͉̂��̂��A���̊T�O��4��(b)�Ő������Ă��܂��B �܂��A���S8�x�E5�x�E4�x�A�ȂǓx���̌Ăѕ��ɂ��ẮA7��[2](-2)�Ő������Ă��܂��B 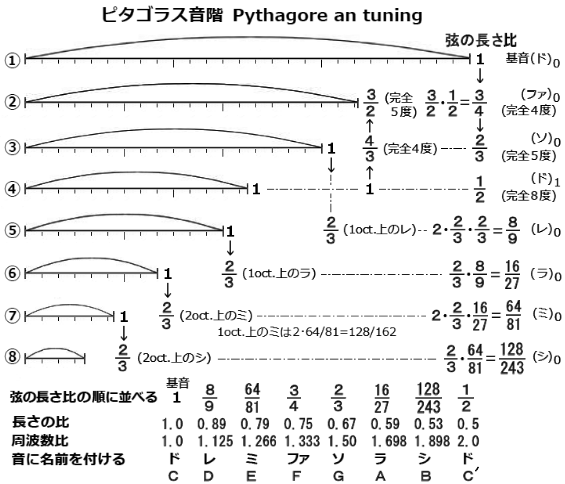 ����̌��̒����@���P�Ƃ��A���̊�ɂ悭���a����2/3�{�̌��B�����B
����̌��̒����@���P�Ƃ��A���̊�ɂ悭���a����2/3�{�̌��B�����B�����ɇB�̌��̒������P�Ƃ��āA���̉��ɂ悭���a����2/3�{�̌��D�����B ������ɇD�̒������P�Ƃ��āA����2/3�{�̌��E�����B ���������E�̒������P�Ƃ��āA����2/3�{�̌��F�����B ���������F�̒������P�Ƃ��āA����2/3�{�̌��G�����B �����ɁA�@�̒������P�Ƃ��āA����1/2�{�̌��C�����B ���Ō�ɁA�C�̒������P�Ƃ��āA����3/2�{�̌��A�����B(�����́A�@�̒�����3/4�{�̌��A)�B�E�E�E �@���̂悤�ɂ��č�����A�@�A�B�A�D�A�E�A�F�A�G�A�C�A�A ���������i���g����͂��̋t���j�ɕ��ׂ��A�u�h���~�t�@�\���V�h�v�̖��O��t������s�^�S���X���K���������܂��B ���̎��_�ɗ����Ă݂�ƁA�ȑO���猾���Ă����A���̒����P�̉����h�̂Ƃ��A����2/3�{�̒����̌��̉����\�A�X�ɂ���2/3�{�m(2/3)X(2/3)=(8/9)X(1/2)�n�̒����̌��̉������ɂȂ邱�Ƃ��悭����܂��B ���āA���̒���������2/3�{���Ȃ��特�K�����߂Ă���ƁA���ۂɂ͇G�̑����������A�G�̌��̒������P�Ƃ����Ƃ�����2/3�{�̉��̓t�@���ɂȂ�܂��B ����Ɍ��̒���������2/3�{���Ă����ƁA�u�t�@�����\�����������������t�@���P�I�N�^�[�u��̃h�v�Ƃ����悤�ɂP�I�N�^�[�u����12���K�����ׂČ��܂�܂��B �@(��) ���K�̒��ŁA�~-�t�@�ԁA�V-�h�Ԃ������Ȃ̂́A�Ȃ��H �@���y�̕����n�߂����A�~-�t�@�A�V-�h�Ԃ������ɂȂ��Ă��邱�Ƃ����炸�A���₵�Ă��v�̂̓��Ȃ����������Ԃ��Ă��Ȃ������B �������A�����ł͂����藝���ł��܂����B �@��}�ŗד��m�̎��g����̍����Ƃ��Ă݂�ƁAD�`C�Ԃ̎��g�����8:9(=8/9:1/1)�A F�`E�Ԃ�243:256(=3/4:64/81=3X81:4X64)�AB�`A�Ԃ�8:9(=128/243:16/27)�AG�`F�Ԃ�8:9(=2/3:3/4)�A �E�E�E�AC'�`B�Ԃ�243:256(=1/2:128/243)�A���̂��Ƃ���A�~�ƃt�@(E:F)�A �V�ƃh(B:C')�̊Ԃ͈�v���A���̗ד��m�̎��g����ɔ�ׂĂقڔ����ɂȂ��Ă��邱�Ƃ�����܂��B ������Q�ӏ��������ɂȂ��Ă��邱�Ƃ́A���̐��藧���Ⓑ���K�^�Z���K�𗝉����邤���ő���Ȃ̂ŁA����ɂ��Ă͉��߂�14�͂Ő������܂��B 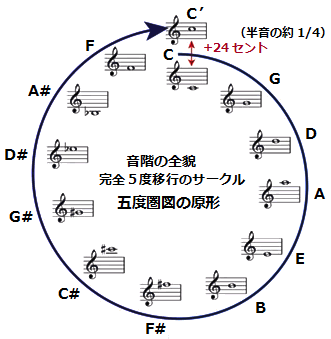 �@�ȏ��Z�߂Ă݂�ƁA�����K�̏ꍇ�̓h����Ƃ��āA���S5�x(���g����2:3)���ςݏグ��ƁA�h�����܂�Έ�`�I�Ƀ\�����܂�A�\�����܂�������܂�B
�@�ȏ��Z�߂Ă݂�ƁA�����K�̏ꍇ�̓h����Ƃ��āA���S5�x(���g����2:3)���ςݏグ��ƁA�h�����܂�Έ�`�I�Ƀ\�����܂�A�\�����܂�������܂�B���l�ɁA�������A�����~�A�~���V�A�V���t�@#�A �t�@#���h���A��#���\#�A�\#����#�A��#����#�A ��#���t�@�A�t�@���h�A�̏��ɉ������܂�A�Ō��12�Ԗڂ̃t�@�����܂��āA�h�ɖ߂��B �@�����12���K�����������ƂɂȂ�A�s�^�S���X�����̒a���ł��B ������2600�N���O�̃s�^�S���X�̎���ɂ́A���g����͂̊T�O�͖����B ����Ȏ���ɁA���̒����u3:2�v�䗦�����𗘗p���ĉ��K�������������̂ł��B �@�܂�A���̑�������g����ŕ\�����u2:3�v�ł���A���̎��g����̉��݂͌��ɂ悭���a�i���S5�x�j���邱�Ƃ���A ����珇���A�T�x�ςݏグ�Ă�����12���K����������Ƃ����P���Ȃ��̂ł����B �i�x���̐������́A7��[2]�����̘b ���������������j �@������~�`��ɕ\���ƁA�����K�̏ꍇ�́u�b�v����ɁA���v���ɏ����T�x�ςݏグ�Ă����Ə�}�̉~��`�����Ƃ��ł��܂��B���ꂪ15�͂ň����ܓx���}�̌��`�ł��B �Ƃ��낪�A��������Ă�������悤�Ɍ݂��ɒ��a���鉹�����߂Ĉꏄ�����Ƃ��A12�Ԗڂ̂b�f�͖{���Ȃ�ŏ��̂b���2�{�̎��g���ɂȂ�͂����A���߂ɋ����Ă����A ���̍���24�Z���g(������100�Z���g��)�̌덷���o���B���ꂪ�s�^�S���X�����Ƃ������ƂɂȂ�܂��B �܂�A���g���䂪2:3�̂Q�̉��́A�I�N�^�[�u���ł͂悭���a���邪�A�I�N�^�[�u�Ԃł͒��a���Ȃ����ƂɂȂ�܂��B �i�� �Z���g�ɂ��Ă�6�͎Q�Ɓj  �@�@ �@�@
  �U�D���ω����Ə��������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@���ꂼ��̕��݂Ɠ���
�U�D���ω����Ə��������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@���ꂼ��̕��݂Ɠ��� �V�D�e�����̓����A�����̘b�^���̒��a�Ƃ�
�V�D�e�����̓����A�����̘b�^���̒��a�Ƃ� �W�D���a���E�s���a���ɂ���
�W�D���a���E�s���a���ɂ����@  �X�D���R�ɔ������鉹�͂��ׂĐ����g�̑g�ݍ��킹�@�@�@�@�@�@�@ �E�E�E�@�{���̒a��
�X�D���R�ɔ������鉹�͂��ׂĐ����g�̑g�ݍ��킹�@�@�@�@�@�@�@ �E�E�E�@�{���̒a�� 10�D�n�[���j�b�N�i�����g�E�{���E���a�j�� �{����
10�D�n�[���j�b�N�i�����g�E�{���E���a�j�� �{���� 11�D������������߁A�{�������F�����߂�
11�D������������߁A�{�������F�����߂� 12�D�a���E�����E���Ȃ艹�E�n�[���j�[�@�@�@�@�@ �E�E�E�@�����̓�F�Y��ȉ��ƌ��ȉ�
12�D�a���E�����E���Ȃ艹�E�n�[���j�[�@�@�@�@�@ �E�E�E�@�����̓�F�Y��ȉ��ƌ��ȉ� 13�D���U�E���E�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E�@�Q�y���̔@��
13�D���U�E���E�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E�@�Q�y���̔@�� 14�D���̐��藧���F�e�g���E�R�[�h�iTetraChord�j�@�@�@�@�@�@�E�E�E�@�Z���K�̓�
14�D���̐��藧���F�e�g���E�R�[�h�iTetraChord�j�@�@�@�@�@�@�E�E�E�@�Z���K�̓� 15�D�ܓx���}�E�����ƗՎ��L��
15�D�ܓx���}�E�����ƗՎ��L�� |