 (卓上の音楽) |
音楽の原点を探る |
画像加工広場 老夫婦の旅記録 |
１．背 景普段の会話で当たり前のように飛び交う言葉の中にも解らないことが沢山ある。音階ができた背景は？、美しい音色とは？、音色を決める倍音の正体は？、ハーモニーの正体は？、 楽しい／悲しい響きとは？、楽曲の仕組みは？、等々、関心ごとは沢山あり、これらを自然現象の中から学ぼうとした。 人は、本能のままに音楽との繋がりを築いてきた。ならば音楽は人為的に考えられた約束事ではなく、自然現象の中から生まれた事象だろうと推察できる。 たとえば、５度の調和、倍音列の響き、差音のハーモニー、規則的リズムの中の不規則な揺らぎ、など、音楽の原点が自然法則の中にある。 その自然法則というのは実に合理的に出来ており、足し算より引き算の美意識の方が合理性に叶う。 そう考えると、音楽ありきで総花的に学ぶより、身近な自然現象の中から音楽を学んだ方が、理解が深まることを実感した。 そこで、これまで断片的に得た音楽の知識を、復習と整理を兼ねて備忘録のつもりで纏めてみました。
２．自然現象の中から音楽を学ぶと理解しやすい ・・・ 音楽と人の本能
３．和む音には、不規則な揺らぎがある ・・・ Simple is Best
４．鍛冶屋の鉄打つ音から音楽の存在を予想 ・・・ ピタゴラス音律の誕生
５．ピタゴラス音律 ・・・ ミ-ファ、シ-ド間が半音なのは？
６．平均音律と純正音律 ・・・ それぞれの歩みと特徴
７．各音律の特徴、音程の話／音の調和とは
８．協和音・不協和音について
９．自然に発生する音はすべて正弦波の組み合わせ ・・・ 倍音の誕生
10．ハーモニック（高調波・倍音・調和）と 倍音列ハーモニックという言葉を調べると、物理では高調波、 数学では（関数の）調和、音楽では倍音・音の調和、などの意味で使われていますが、どういう意味か、自然に発生する音で考えると解りやすい。 前の9章では、世の中のあらゆる音はすべて正弦波の組み合わせで表せると言ってましたが、 太鼓やドラのような平面楽器、しゃがれ声、ささやき声、声帯を傷めたような声などは、もっと複雑で簡単な整数比では表せないノイズが発生します。 これは3章で扱った、ホワイトノイズです。ある基音の整数倍、云々の話ではなく、全くの独立したランダムノイズです。 演奏を聴いている隣で、ガシャガシャ喋り声が聞こえたとすれば、これも関係のないノイズです。  9章で述べたように自然に発生する音や組織的に創られた楽器音は、 基音(f)の他、倍音(2f、3f、･･･)に分解できるが、それ以外の音が発生することもあり、 その音の強さは、およそ図のような関係になり、この周波数分布の形によって音色が変わると云うことです。 図のような関係を調べることを周波数解析といい、楽器や演奏の音色の評価に役立っています。 上図を見て分かるように、自然音では基音が最も強く、次数が増えるほど倍音は次第に減衰していきます。 しかし、逆の場合もあります。たとえば、赤ちゃんの泣き声では基音より倍音のほうがかなり強く出ます。 また、楽器などで創られた音も、共鳴などで音の出し方によっては基音より倍音のほうが強く出る場合が多くあります。 次に、ある特定音を鳴らしたとき、どのような倍音が同時に鳴るか、例を使って説明します。 基音に対して倍音は、偶数倍か、奇数倍か、それぞれの倍音の含まれ方によって音色に差が生じます。 ある基音から始まって、その音を基準にその整数倍の音を順に並べたものを倍音列と呼んでいます。 6章の純正音律では、基準音の周波数の整数倍（自然倍音）を用いて、うなりが発生しない美しい和音を作るように音階を定めました。 その音階は、互いによく調和する音同士の周波数比で決めました。 ここでは、基音とその整数倍音との周波数比で倍音列を決めています。まず次の表を見てください。 倍音１（ユニゾン）のド1を基音として、その基音が16倍音まで再生された場合、各倍音はどのような音になるか、音名で示しています。 （たとえば、2倍音は基音の1オクターブ上のド、3倍音は1オクターブ上のソ）
では、倍音が上表のような音名になるのは何故か。次のように説明できます。 まず、基音Ｃ1(ド1)の2倍音は１オクターブ上の音だからＣ2（ド2）です。 基音の２のn乗の音は、nオクターブ上の音なので、2,4,8,16倍音の音は1,2,3,4オクターブ上のド音になります。 たとえば、３オクターブ上のド音はC4です。 （尚、なぜオクターブという単位なのか、については4章で説明しています。） 次に、その他の倍音はどういう音になるか。 先ず、2倍音と3倍音との周波数比は、2:3 だから、3倍音は2倍音の(3/2)倍の周波数になる。 これは、Ｂ表純正音律（6章で求めた表）を参考に見るとＧに相当します。 したがって、Ａ表の3倍音はＧ2になります。Ｇ2は基音Ｃ1の１オクターブ上のソの意味です。
同様に、5倍音は4倍音の(5/4)倍 → Ｂ表のＥ → Ａ表5倍音はＥ3。 6倍音は4倍音の(6/4=3/2)倍 → Ａ表6倍音はＧ3。7倍音は4倍音の(7/4)倍 → Ａ表7倍音は？。 9倍音は8倍音の(9/8)倍 → 9倍音はＤ4。10倍音は8倍音の(10/8=5/4)倍 → 10倍音はＥ4。 11倍音は8倍音の(11/8)倍 → 11倍音は？。12倍音は8倍音の(12/8=3/2)倍 → 12倍音はＧ4。 13倍音は8倍音の(13/8)倍 → 13倍音は？。14倍音は8倍音の(14/8=7/4)倍 → 14倍音は？。 15倍音は8倍音の(15/8)倍 → 15倍音はＢ4。 ここで、？が幾つか出てきました。 これはＢ表では決まらないが、オクターブ12個の半音の何れかの値で、♭・＃を伴う音であることだけは理解できます。 故に、第7倍音の場合は、A(5/3) ＜ ？(7/4) ＜ B(15/8)で、ラ～シの間の音であるから、？はシ♭、 同様に、11倍音は、F(4/3) ＜ ？(11/8) ＜ G(3/2)で、ファ～ソの間の音であるから、ファ＃、 13倍音は、G(3/2) ＜ ？(13/8) ＜ A(5/3)で、ソ～ラの間の音であるから、ソ＃かラ♭、になります。 純正律を使う楽器では、 ＃と♭では微妙に違ってくるので使い分けていますが、 例外的に各調のファ♯とシ♭だけは上向き、下向きに関わらず、この表記で表します。 （＃・♭の使い分けは、15章(-1)参照） したがって、結論的には上記Ａ表のような倍音列が完成するのです。 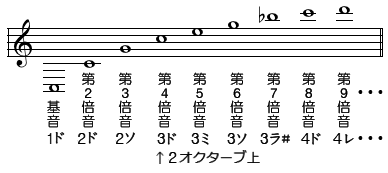 上記Ａ表の倍音列に戻って、これを五線譜で表すと右図のようになります。 ここから分かることは、基音（1ド）を鳴らすと、大小に関わらず１オクターブ上の2ド・ソ、２オクターブ上の3ド・ミ・ソ・・・、の音も同時に鳴っていることになります。 この章の冒頭で説明したように、一般には、倍音の次数が多くなるほど音量は次第に減衰していきますが、 ある倍音が他の周波数と共鳴することがあれば、その倍音は逆に強くなることもあります。 たとえば、前述の赤ちゃんの泣き声、楽器でも音の出し方によっては倍音のほうが強くなる。 ピアノの音は鳴らした瞬間から減衰がはじまる楽器なので、基音を鳴らした後に伸びてゆく音を聴くと、倍音が鳴っていることがよく解ります。 この倍音の出方は楽器によって異なり、フルートやピアノのような柔らかい音の楽器は一般には倍音が少な目、 弦楽器やクラリネットやサックス、トランペットなどの楽器は、倍音を豊富に含んでいるといわれます。 ハーモニカはリードプレートの振動音なので弦楽器と同様に整数倍音の出やすい楽器です。 楽器の倍音については、改めて11章で詳しい話が出ますが、基音は実際に鳴らす音ですから、基音で音程が決まり、上記のように倍音の数と量で音色が決まることになります。 ■ 倍音が音色を決める例 以上の倍音列について、Ｃ調ハーモニカのド音(C4)を実際に測定してみたときの波形と周波数スペクトルを示します。 上段の波形はド音を出しはじめから17ミリ秒間の波形を拡大にて表示しています。 これを見ると、基音の正弦波だけでなく、多くの倍音が含まれて複雑な波形になっていることが解ります。この波形がこの音の音色になるのです。 次に、下段の周波数スペクトルを見ると、基音(C4≒523Hz)のパワーが多く出ていますが、2,3,4,5,6,･･･15倍音もよく出ていることが解ります。 ここでは、特に7倍音(≒3729Hz)のシ♭が、基音ドと同程度に多くのパワーが出ていることが解ります。 つまり、ハーモニカのド音を吹いたところ、このときはシ♭音が多く含まれていたことが解ります。 一般に自然が作り出す音は、基音が最も強く、次数が増えるほど倍音は次第に減衰していくが、下図のように共鳴箱などを通して作られた音は、基音より倍音のほうが強く出る場合が多くあることの証です。  上記と同じド音を、吹き方を少し変えて出したときの周波数スペクトルの例です。前記とは少し様子が違って、5倍音(≒2637Hz：ミ)・6倍音(≒3136Hz：ソ)が基音より大きい値になっています。 つまり、ハーモニカのド音を吹いたところ、先ほどとは違ってミ音･ソ音が多く含まれていたことが解ります。 ここで言えることは、同じ音を出したつもりでも、吹き方によって音色がずいぶん違ってくるということです。 音程と音色については11章で詳しく説明します。 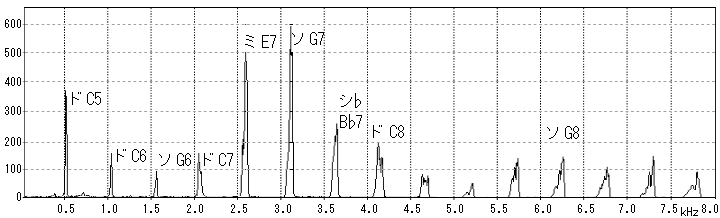 ■ 音の種類は、・・・これまでの纏め （詳しくは11章で説明します） ①基音：楽器音の基本になっている周波数（正弦波）の音で、これで音の高さ（音程）を感じる。 これだけでは楽器の音にはならず、単に時報や電子音などの単純な音のように聴こえる。 ②整数倍音：基音の整数倍の周波数の音で、第２倍音、第３倍音・・・・高い音まで発生するが、一般には次数が増えるほど次第に減衰するが、上記のように共鳴の仕方で異なる。 人の耳には聞こえる範囲は若年層でも20Hz～20KHzまで。 弦楽器の場合は、弦が振動する際は、弦の長さで振動、その半分で振動、そのまた半分で振動・・・の現象があるので、 整数倍音は弦の振動によって容易に生み出される。 フルートやピアノなどでは、逆に倍音の発生を抑え、柔らかく優しい音色を表現しているようです。 ③非整数倍音：音程とは関係なく独立して鳴っている音で、ドラを鳴らすと「ジャ～～～ン！！」とすごい音がするが、 整数倍音のような規則的な音ではなく不規則な音が同時に鳴っている。これはホワイトノイズ。 
11．基音が音程を決め、倍音が音色を決める
12．和音・差音・うなり音・ハーモニー ・・・ 差音の謎：綺麗な音と嫌な音
13．共振・共鳴・同調 ・・・ 群軽折軸の如く
14．調の成り立ち：テトラ・コード（TetraChord） ・・・ 短音階の謎
15．五度圏図・調号と臨時記号 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright ©2019 - Smo. All rights reserved. Last Updated 09/18/2019.