 (卓上の音楽) |
音楽の原点を探る |
画像加工広場 老夫婦の旅記録 |
１．背 景普段の会話で当たり前のように飛び交う言葉の中にも解らないことが沢山ある。音階ができた背景は？、美しい音色とは？、音色を決める倍音の正体は？、ハーモニーの正体は？、 楽しい／悲しい響きとは？、楽曲の仕組みは？、等々、関心ごとは沢山あり、これらを自然現象の中から学ぼうとした。 人は、本能のままに音楽との繋がりを築いてきた。ならば音楽は人為的に考えられた約束事ではなく、自然現象の中から生まれた事象だろうと推察できる。 たとえば、５度の調和、倍音列の響き、差音のハーモニー、規則的リズムの中の不規則な揺らぎ、など、音楽の原点が自然法則の中にある。 その自然法則というのは実に合理的に出来ており、足し算より引き算の美意識の方が合理性に叶う。 そう考えると、音楽ありきで総花的に学ぶより、身近な自然現象の中から音楽を学んだ方が、理解が深まることを実感した。 そこで、これまで断片的に得た音楽の知識を、復習と整理を兼ねて備忘録のつもりで纏めてみました。
２．自然現象の中から音楽を学ぶと理解しやすい ・・・ 音楽と人の本能
３．和む音には、不規則な揺らぎがある ・・・ Simple is Best
４．鍛冶屋の鉄打つ音から音楽の存在を予想 ・・・ ピタゴラス音律の誕生
５．ピタゴラス音律 ・・・ ミ-ファ、シ-ド間が半音なのは？
６．平均音律と純正音律 ・・・ それぞれの歩みと特徴
７．各音律の特徴、音程の話／音の調和とは２音間で美しい響きが得られる音律を求めても全てを満たす訳ではないが、 調和しないからといって、嫌な音かと云えば、そうではない。 調和しない音でも、流れの中では緊張感を持った心地よい印象を与えることもあるので、先ずは各音律を整理し、その中で各音程の響きを見ていきます。 ［１］．各音律の特徴（要約） 先ずは、5章、6章で詳しく説明してきた各音律の特徴を纏めると以下のようになります。 ■ ピタゴラス音律 ２つの音を同時に鳴らしたとき、その周波数比(音程比)が1:2、2:3、3:4のときよく調和することだけを利用して12音階を定めている。 実際は、基準音に対して周波数比が2:3になる音を積み上げて12音階を作っているので、１オクターブの範囲内であれば２つの音は最もよく調和する。 ところが、互いに調和する音を自動的に積み上げたため、オクターブ間で誤差が生じて周波数比が1:2にならない。 たとえば、ド音と１オクターブ上のド音の周波数比が1:2にならないという問題が生じて、オクターブ間で調子外れに響かせてしまう。つまり、オクターブ間では移調・転調には向かない。 ■ 平均音律 バロック時代のバッハが平均音律を確立したといわれる。 ピタゴラス音律で一致しなかったオクターブの響きだけはぴったり合わせようと、オクターブ間の誤差を各音に均等に２セントずつ割り振るという単純な方法で音階を定めた。 その結果、オクターブ内の２音間ではピタゴラス音律ほど調和しなくなったが、それは許容範囲であり、それよりオクターブ間の周波数比が1:2になるようにしたことで、オクターブ間の響きにうなりは無くなり、 さらに任意の調へ移調・転調することが可能になった。 ■ 純正音律 最も調和する周波数比2:3(完全5度)と、次に調和する周波数比4:5(長3度)だけを用いて長音階を決め、 周波数比2:3(完全5度)と5:6(短3度)を用いて短音階を決めている。 この周波数比で各音を割り振っているので、調和音だけが得られるかに見えるが、完全5度でありながら調和しない音が出てきた。 つまり、オクターブ内で特定の音の組み合わせで調和するが、他の組み合わせで濁った音程も存在する。 その理由は、音程の割り振り方にあり、半音Ｘ２ ≠ 全音。さらに、全音には２種類の響きがあるため、たとえば、Ｃ＃とＢ♭は同じ音にはならない。 その結果、純正音律は移調・転調に向かないということになるが、純正音律を使う楽器では、これ等は演奏者によって調整されるという。 ■ 各種楽器で使われる音律 平均音律は、ピアノ、オルガン、木琴、ハーモニカのように、 音の出る位置が決まっている楽器に用いられています。（ここでは、＃ドと♭レは同じ音になる。） 純正音律は、フルート、バイオリン、三味線、トランペットのように、 吹き方や弦を押さえる指の位置で音程を自由に修正でき、その音程も整数比で保つことができるような楽器に用いられているそうです。 （たとえば、＃ドと♭レは違う音で演奏される。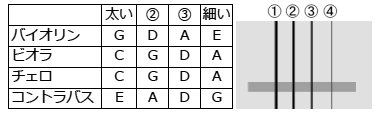）  ついでに、弦楽器の開放弦の音について調べてみました。 開放弦とは、どこも押さえずに弾いた時に出る音のことで、この音を基準に、どこを押さえると何の音が出るのか決まる。 ４弦の構成は右表の通りで、これを見ると、コントラバス以外は弦の隣間が完全5度になっており、コントラバスだけは完全4度になっています。（音の並びがバイオリンの逆になっている） ［２］．音程の話／音の調和とは 複数の音を同時に鳴らしたとき、よく調和するとか、ハモるとか、ビート音とか、言葉だけはよく飛び交うが、これらは一体何者か。 これ等すべてが音波の重なりの延長上にあるで話は分かりやすい。 （-１）音の調和とは （詳細は12章で） 12章で、波の重なり具合を図解しながら詳しく説明するので、ここでは要約だけにしておきます。 調和するとは、２つの音の周波数が互いに重なり合うことで、 完全に重なれば周波数比1:1の一つの音になり、音量は増すが音の広がりは無い。単純な周波数比（たとえば、2:3）で重なれば２音はよく調和音し、音域も広がりを持つようになる。 一方、互いの周波数がうまく重ならないで、１秒間に20回程度以下の割合で稀に重なると、それはうなり（ビート）音になる。 複音ハーモニカのトレモロはうなり音で、たとえばＡｍのハーモニカでは、2Hz(C3)〜16Hz(C6)の範囲でうなり音が生じます。 繰り返して言えば、音の調和とは、２つの音から和音（chord）を作ったとき、その２つの音の重なり具合のことで、 その重なり具合は、２つの周波数の差に等しい新たな音になって現れます。 この新たに発生する音、つまり差音が、うなり(beat)音／協和音／不協和音の何れかになります。 どういうことか、12章で図解しながら詳しく説明するので、ここでは話を先に進めます。 （-２）音程の話、度数の数え方 ２つの音の間隔のことを『音程』といい、その間隔を度数という単位で表す。 
度数の数え方は、図のように基音の位置を一度と数えます。♯や♭などの臨時記号がついた派生音がある場合も度数の数え方は変わらないので、『同じ度数でも響き方が違う』という音程ができます。 この響きの違いは、長短・増減で表し、たとえば、同じ２度でも長２度、短２度のように表現されます。 （-３）音程の種類 ２つの音の間隔に全音･半音がいくつ含まれるかによって、完全音程、長音程、短音程、増音程、減音程の５つに分類されます。 但し、この半音・全音は、ハ長調の音列であるテトラ・コード(全音・全音・半音・全音・全音・半音)を基準にしており、その音程は、以下のように１度〜８度までの度数で決められています。 （完全系・長短系、増減系音程については、8章の協和・不協和音の種類で説明しています） 尚、テトラ・コードは、調の成り立ちに重要な役割をもつので、改めて14章で詳しく説明します。  ◆１度の音程：１度（ユニゾン）は同じ音で、周波数比が(1:1)だから、常に完全１度しか存在しない。 ◆２度の音程：２つの音の間が、半音なら短２度、全音なら長２度、の２種類。 この２つの音はまったく溶け合わないため、耳障りな響きになり、俗に”音がぶつかる”という言葉を使っています。 ◆３度の音程：２つの音の間が、全音２つなら長３度、全音と半音１つなら短３度、の２種類。 意外と耳慣れた音なのでよく使われ、基本の和音の一つになっています。 ◆４度の音程：２音間が、２全音半なら完全４度、３全音なら増４度（ファ〜シ）、の２種類。 ◆５度の音程：２音間が、３全音半なら完全５度、２全音＋２半音なら減５度（シ〜ファ）、の２種類。 増4度と減5度は『音程の転回』と云い、音の性格は同じで響き方が変わる。（8章参照） 完全4度・完全5度の音程はよく調和する安定した和音で、音律成立の原点になっている。 ◆６度の音程：２音間が、４全音＋１半音の長６度と、３全音＋２半音の短６度、の２種類。 周波数比は、長6度が3:5、短6度が5:8で、両者とも不完全協音程で、少し和みのある音。 ◆７度の音程：２音間が、５全音＋１半音の長７度、４全音＋２半音の短７度、の２種類。 不協和音程でありながら、特に短7度はセブンス・コードとしてよく使われます。 ◆８度の音程：２音間が、１オクターブは音の周波数比が1:2になるので完全協音程で、完全８度のみ。 ※：以上は８章で、完全系、長短系、増減・重増減、に細分化して詳しく説明しています。 
８．協和音・不協和音について
９．自然に発生する音はすべて正弦波の組み合わせ ・・・ 倍音の誕生
10．ハーモニック（高調波・倍音・調和）と 倍音列
11．基音が音程を決め、倍音が音色を決める
12．和音・差音・うなり音・ハーモニー ・・・ 差音の謎：綺麗な音と嫌な音
13．共振・共鳴・同調 ・・・ 群軽折軸の如く
14．調の成り立ち：テトラ・コード（TetraChord） ・・・ 短音階の謎
15．五度圏図・調号と臨時記号 |
Copyright ©2019 - Smo. All rights reserved. Last Updated 09/18/2019.