 (‘ىڈم‚ج‰¹ٹy) |
پ@‰¹ٹy‚جŒ´“_‚ً’T‚é |
‰و‘œ‰ءچHچLڈê کV•v•w‚ج—·‹Lک^ |
 ‚PپD”w Œi
‚PپD”w Œiپ@•پ’i‚ج‰ïکb‚إ“–‚½‚è‘O‚ج‚و‚¤‚ة”ٍ‚رŒً‚¤Œ¾—t‚ج’†‚ة‚à‰ً‚ç‚ب‚¢‚±‚ئ‚ھ‘ٍژR‚ ‚éپB‰¹ٹK‚ھ‚إ‚«‚½”wŒi‚حپHپA”ü‚µ‚¢‰¹گF‚ئ‚حپHپA‰¹گF‚ًŒˆ‚ك‚é”{‰¹‚جگ³‘ج‚حپHپAƒnپ[ƒ‚ƒjپ[‚جگ³‘ج‚حپHپA ٹy‚µ‚¢پ^”ك‚µ‚¢‹؟‚«‚ئ‚حپHپAٹy‹ب‚جژd‘g‚ف‚حپHپA“™پXپAٹضگS‚²‚ئ‚ح‘ٍژR‚ ‚èپA‚±‚ê‚ç‚ًژ©‘RŒ»ڈغ‚ج’†‚©‚çٹw‚ع‚¤‚ئ‚µ‚½پB پ@گl‚حپA–{”\‚ج‚ـ‚ـ‚ة‰¹ٹy‚ئ‚جŒq‚ھ‚è‚ً’z‚¢‚ؤ‚«‚½پB‚ب‚ç‚خ‰¹ٹy‚حگlˆ×“I‚ةچl‚¦‚ç‚ꂽ–ٌ‘©ژ–‚إ‚ح‚ب‚پAژ©‘RŒ»ڈغ‚ج’†‚©‚çگ¶‚ـ‚ꂽژ–ڈغ‚¾‚낤‚ئگ„ژ@‚إ‚«‚éپB ‚½‚ئ‚¦‚خپA‚T“x‚ج’²کaپA”{‰¹—ٌ‚ج‹؟‚«پAچ·‰¹‚جƒnپ[ƒ‚ƒjپ[پA‹K‘¥“IƒٹƒYƒ€‚ج’†‚ج•s‹K‘¥‚ب—h‚炬پA‚ب‚اپA‰¹ٹy‚جŒ´“_‚ھژ©‘R–@‘¥‚ج’†‚ة‚ ‚éپB ‚»‚جژ©‘R–@‘¥‚ئ‚¢‚¤‚ج‚حژہ‚ةچ‡—“I‚ةڈo—ˆ‚ؤ‚¨‚èپA‘«‚µژZ‚و‚èˆّ‚«ژZ‚ج”üˆسژ¯‚ج•û‚ھچ‡—گ«‚ةٹگ‚¤پB ‚»‚¤چl‚¦‚é‚ئپA‰¹ٹy‚ ‚è‚«‚إ‘چ‰ش“I‚ةٹw‚ش‚و‚èپAگg‹ك‚بژ©‘RŒ»ڈغ‚ج’†‚©‚特ٹy‚ًٹw‚ٌ‚¾•û‚ھپA—‰ً‚ھگ[‚ـ‚邱‚ئ‚ًژہٹ´‚µ‚½پB ‚»‚±‚إپA‚±‚ê‚ـ‚إ’f•ذ“I‚ة“¾‚½‰¹ٹy‚ج’mژ¯‚ًپA•œڈK‚ئگ®—‚ًŒ“‚ث‚ؤ”ُ–Yک^‚ج‚آ‚à‚è‚إ“Z‚ك‚ؤ‚ف‚ـ‚µ‚½پB  ‚QپDژ©‘RŒ»ڈغ‚ج’†‚©‚特ٹy‚ًٹw‚ش‚ئ—‰ً‚µ‚â‚·‚¢پ@پ@پ@پ@پ@پ@پ@پEپEپEپ@‰¹ٹy‚ئگl‚ج–{”\
‚QپDژ©‘RŒ»ڈغ‚ج’†‚©‚特ٹy‚ًٹw‚ش‚ئ—‰ً‚µ‚â‚·‚¢پ@پ@پ@پ@پ@پ@پ@پEپEپEپ@‰¹ٹy‚ئگl‚ج–{”\ ‚RپDکa‚ق‰¹‚ة‚حپA•s‹K‘¥‚ب—h‚炬‚ھ‚ ‚éپ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@ پEپEپEپ@Simple is Best
‚RپDکa‚ق‰¹‚ة‚حپA•s‹K‘¥‚ب—h‚炬‚ھ‚ ‚éپ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@ پEپEپEپ@Simple is Best ‚SپD’b–艮‚ج“S‘إ‚آ‰¹‚©‚特ٹy‚ج‘¶چف‚ً—\‘z پ@پ@پ@پ@پ@پ@ پEپEپEپ@ƒsƒ^ƒSƒ‰ƒX‰¹—¥‚ج’aگ¶
‚SپD’b–艮‚ج“S‘إ‚آ‰¹‚©‚特ٹy‚ج‘¶چف‚ً—\‘z پ@پ@پ@پ@پ@پ@ پEپEپEپ@ƒsƒ^ƒSƒ‰ƒX‰¹—¥‚ج’aگ¶ ‚TپDƒsƒ^ƒSƒ‰ƒX‰¹—¥پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@ پEپEپEپ@ƒ~-ƒtƒ@پAƒV-ƒhٹش‚ھ”¼‰¹‚ب‚ج‚حپH
‚TپDƒsƒ^ƒSƒ‰ƒX‰¹—¥پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@ پEپEپEپ@ƒ~-ƒtƒ@پAƒV-ƒhٹش‚ھ”¼‰¹‚ب‚ج‚حپH ‚UپD•½‹د‰¹—¥‚ئڈƒگ³‰¹—¥
‚UپD•½‹د‰¹—¥‚ئڈƒگ³‰¹—¥پ@ژ‘م‚ح‰ك‚¬‚ؤ11گ¢‹I‚²‚ë‚©‚çپAˆê‚آ‚جگù—¥‚ًƒ†ƒjƒ]ƒ“‚¾‚¯‚إ‚ب‚‚S“xپA‚T“xپA‚W“x‚إڈd‚ث‚ؤ‰ج‚¤‘½گ؛‰¹ٹy‚ھƒsƒ^ƒSƒ‰ƒXگù—¥‚ة‚و‚ء‚ؤ—p‚¢‚ç‚ê‚ؤ‚¢‚½پB پi“xگ”‚جگ”‚¦•û‚حپA7ڈح[2]‰¹’ِ‚جکb ‚إگà–¾‚µ‚ـ‚·پj ‚ئ‚±‚ë‚ھپA14گ¢‹IŒم”¼‚²‚ëپA‹³‰ï‚ً’†گS‚ة‰¹ˆو‚جچL‚¢‘½گ؛‰¹ٹy‚ھگi“W‚·‚é‚ئپAƒsƒ^ƒSƒ‰ƒX‰¹—¥‚إ‚حƒIƒNƒ^پ[ƒuٹش‚إ’²ژqٹO‚ê‚ة‹؟‚©‚¹‚ؤ‚µ‚ـ‚¤‚±‚ئ‚ھ–â‘è‚ة‚ب‚ء‚ؤ‚«‚½‚»‚¤‚إ‚·پB پ@ƒsƒ^ƒSƒ‰ƒX‰¹—¥‚ج’aگ¶‚©‚ç2000”N‹ك‚Œم‚جپA16گ¢‹I‚²‚ë‚ة‚ب‚ء‚ؤپAƒsƒ^ƒSƒ‰ƒX‰¹—¥‚جƒIƒNƒ^پ[ƒuٹش‚ج‹؟‚«‚¾‚¯‚ح‚ز‚ء‚½‚èچ‡‚ي‚¹‚و‚¤‚ئچl‚¦‚é‚و‚¤‚ة‚ب‚èپA‚±‚±‚ة•½‹د‰¹—¥‚ھ’aگ¶‚µ‚ـ‚µ‚½پB پ@ˆê•ûپA‚»‚ج‘O‚ج15گ¢‹I‚²‚ë‚ة‚حپA‚»‚ج‘½گ؛‰¹ٹy‚à•،ژG‰»‚µپA•ت‚ج“®‚«‚ئ‚µ‚ؤپA‚R“xپA‚U“x‚ج‰¹’ِ‚à‚«‚ê‚¢‚ة‹؟‚‰¹—¥‚ھچl‚¦‚ç‚ê‚é‚و‚¤‚ة‚ب‚èپAڈƒگ³‰¹—¥‚ض‚ئ”“W‚µ‚ؤ‚¢‚ء‚½‚و‚¤‚إ‚·پB پ@پi‚Pپj•½‹د‰¹—¥ پ@•½‹د‰¹—¥‚ًچإڈ‰‚ةژg‚¢‚ح‚¶‚ك‚½‚ج‚حپA‰¹ٹy‚ج•ƒ‚ئڈج‚³‚ê‚éƒoƒbƒn(ƒoƒچƒbƒN‰¹ٹyژ‘م)‚¾‚ء‚½‚»‚¤‚إ‚·پB  ‘Oڈq5ڈح‚جƒsƒ^ƒSƒ‰ƒX‰¹—¥‚إ‚حپAŒف‚¢‚ة’²کa‚·‚鉹‚ً‹پ‚ك‚ؤˆêڈ„‚·‚é‚ئپA13”ش–ع(1ƒIƒNƒ^پ[ƒuڈم)‚ج‚b' ‚حپAچإڈ‰‚ج‚b‚ج‚Q”{‚و‚èچ‚‚ك‚ة‹¶‚ء‚ؤ‚¨‚èپA ‚»‚جچ·24ƒZƒ“ƒg‚جŒëچ·(”¼‰¹پپ100ƒZƒ“ƒgپ¦)‚ھڈo‚ؤ‚µ‚ـ‚¤پB
‚±‚ج—]‚è24ƒZƒ“ƒg‚ً12Œآ‚ة‹د“™‚ةٹ„‚èگU‚ء‚ؤپA‚b‚ئ‚b' ‚ج‚¸‚ê‚ً–³‚‚µ‚½‚ج‚ھ•½‹د‰¹—¥‚إ‚·پB
‚آ‚ـ‚èپA‚±‚ج—]‚è‚ًƒsƒ^ƒSƒ‰ƒX‰¹—¥‚جٹe‰¹‚ةٹ„‚èگU‚ء‚½‚±‚ئ‚ة‚و‚èپAƒIƒNƒ^پ[ƒuٹش‚ج‹؟‚«‚ة‚¤‚ب‚è‚ھ–³‚‚ب‚èپA
‚±‚ê‚ة‚و‚ء‚ؤ”Cˆس‚ج’²‚ة“]’²‚·‚邱‚ئ‚ھ‰آ”\‚ة‚ب‚ء‚½پB‚±‚ê‚ھ•½‹د‰¹—¥‚جچإ‘ه‚جƒپƒٹƒbƒg‚إ‚·پB
‘Oڈq5ڈح‚جƒsƒ^ƒSƒ‰ƒX‰¹—¥‚إ‚حپAŒف‚¢‚ة’²کa‚·‚鉹‚ً‹پ‚ك‚ؤˆêڈ„‚·‚é‚ئپA13”ش–ع(1ƒIƒNƒ^پ[ƒuڈم)‚ج‚b' ‚حپAچإڈ‰‚ج‚b‚ج‚Q”{‚و‚èچ‚‚ك‚ة‹¶‚ء‚ؤ‚¨‚èپA ‚»‚جچ·24ƒZƒ“ƒg‚جŒëچ·(”¼‰¹پپ100ƒZƒ“ƒgپ¦)‚ھڈo‚ؤ‚µ‚ـ‚¤پB
‚±‚ج—]‚è24ƒZƒ“ƒg‚ً12Œآ‚ة‹د“™‚ةٹ„‚èگU‚ء‚ؤپA‚b‚ئ‚b' ‚ج‚¸‚ê‚ً–³‚‚µ‚½‚ج‚ھ•½‹د‰¹—¥‚إ‚·پB
‚آ‚ـ‚èپA‚±‚ج—]‚è‚ًƒsƒ^ƒSƒ‰ƒX‰¹—¥‚جٹe‰¹‚ةٹ„‚èگU‚ء‚½‚±‚ئ‚ة‚و‚èپAƒIƒNƒ^پ[ƒuٹش‚ج‹؟‚«‚ة‚¤‚ب‚è‚ھ–³‚‚ب‚èپA
‚±‚ê‚ة‚و‚ء‚ؤ”Cˆس‚ج’²‚ة“]’²‚·‚邱‚ئ‚ھ‰آ”\‚ة‚ب‚ء‚½پB‚±‚ê‚ھ•½‹د‰¹—¥‚جچإ‘ه‚جƒپƒٹƒbƒg‚إ‚·پB‚»‚ê‚ةپA•½‹د‰¹—¥‚حکa‰¹‚ة‚¤‚ب‚è‚ھ”گ¶‚·‚é‚ئ‰]‚ي‚ê‚é‚ھپAژ¨ڈل‚è‚à‚»‚ê‚ظ‚اˆ«‚‚ب‚¢‚ج‚إچ،‚à—ک—p‚³‚ê‚ؤ‚¢‚ـ‚·پB ‚½‚ئ‚¦‚خپAƒsƒAƒmپAƒIƒ‹ƒKƒ“پA–ط‹صپAƒnپ[ƒ‚ƒjƒJ‚ج‚و‚¤‚ةپA‰¹‚جڈo‚éˆت’u‚ھŒˆ‚ـ‚ء‚ؤ‚¢‚éٹyٹي‚ة‚ح•½‹د‰¹—¥‚ھ—p‚¢‚ç‚ê‚ؤ‚¢‚ـ‚·پB پ@—صژ‹Lچ†پ”پEپَ‚ًژg‚¢•ھ‚¯‚½ٹy•ˆ‚ًŒ©‚©‚¯‚ـ‚·‚ھپA•½‹د‰¹—¥‚ًژg‚¤ٹyٹي‚إ‚حپA‚½‚ئ‚¦‚خپAƒhپ”‚ئƒŒپَ‚ح“¯‚¶‰¹‚ة‚ب‚éپA ‚ئ‚¢‚ء‚½ٹô‚آ‚©‚ج–â‘è“_‚ح‘أ‹¦‚³‚ê‚ؤ‚¢‚é‚و‚¤‚إ‚·پB ‚±‚ê‚ة‘خ‚µ‚ؤپA‰؛‹L‚جڈƒگ³‰¹—¥‚ًچج—p‚·‚éپAŒ·ٹyٹيپAƒtƒ‹پ[ƒgپAƒgƒ‰ƒ“ƒyƒbƒg‚ب‚ا‚حپAگپ‚«•û‚⌷‚ً‰ں‚³‚¦‚éژw‚جˆت’u‚إ‰¹’ِ‚ًژ©—R‚ةڈCگ³‚إ‚«‚é‚ج‚إپA پ”‚ئپَ‚حژg‚¢•ھ‚¯‚ؤ‰‰‘t‚³‚ê‚ؤ‚¢‚é‚و‚¤‚إ‚·پB پ@پ¦ ƒZƒ“ƒg‚ة‚آ‚¢‚ؤپF پ@ƒZƒ“ƒg‚جکb‚ھڈo‚½‚ئ‚±‚ë‚إپA“xگ”‚و‚è‚à‚ء‚ئچׂ©‚¢‰¹’ِ‚ج‰ءŒ¸‚ة‚آ‚¢‚ؤگà–¾‚µ‚ؤ‚¨‚«‚ـ‚·پB گl‚جژ¨‚إ‚ح‰¹’ِ‚جچ·‚حژü”gگ”‚ج”ن‚إ”Fژ¯‚³‚ê‚邽‚كپA ‚½‚ئ‚¦‚خپAپuƒhپEƒ\پvٹش‚حژü”gگ””ن‚إ2:3پAپuƒŒپEƒ~پvٹش‚ح9:10پA‚ج‚و‚¤‚ة•\Œ»‚³‚ê‚é‚ھپA‚±‚ê‚إ‚ح•ھ‚©‚è“ï‚¢‚ج‚إپAƒZƒ“ƒg(cent)‚ئ‚¢‚¤’Pˆت‚ھژg‚ي‚ê‚é‚و‚¤‚ة‚ب‚èپA ‘خگ”ژ²‚إ1ƒIƒNƒ^پ[ƒu‚ً1200“™•ھ‚µ‚ؤپA‚»‚ج’Pˆت‚ًƒZƒ“ƒg‚ئ–¼‚أ‚¯‚ـ‚µ‚½پB ‚±‚ê‚ة‚و‚é‚ئپA1ƒIƒNƒ^پ[ƒu‚ح1200ƒZƒ“ƒgپA•½‹د‰¹—¥‚ج”¼‰¹‚ح100ƒZƒ“ƒgپA“¯‚¶‚ٹ®‘S5“x‚ح700ƒZƒ“ƒgپAڈƒگ³‰¹—¥‚ج5“x‚ح702ƒZƒ“ƒg‚ة‚ب‚éپB ‰¹’ِ‚ج‰ءŒ¸‚àƒZƒ“ƒg’l‚ج‰ءŒ¸‚ة‚و‚ء‚ؤچs‚ي‚êپA’Z2“xپ{’·2“x‚ب‚ç‚خپA100ƒZƒ“ƒgپ{200ƒZƒ“ƒgپپ300ƒZƒ“ƒg‚ئ‚¢‚¤‚و‚¤‚ة‚ب‚è‚ـ‚·پB ژہچغ‚جŒvژZژ®‚إ•\‚ي‚·‚ئپA‚ ‚鉹’ِ”ن‚q‚جƒZƒ“ƒg’l Cent=log(R) / log(2)*1200پj‚ة‚ب‚è‚ـ‚·پB پ@پi‚Qپjڈƒگ³‰¹—¥ پ@ڈƒگ³‰¹—¥‚حپAٹîڈ€‰¹‚جژü”gگ”‚جگ®گ””{پiژ©‘R”{‰¹پj‚ً—p‚¢‚ؤپA‚¤‚ب‚è‚ھ”گ¶‚µ‚ب‚¢”ü‚µ‚¢کa‰¹‚ًچى‚邽‚ك‚ج‰¹ٹK‚إ‚·پB ژه—vژOکa‰¹پiƒhƒ~ƒ\پAƒtƒ@ƒ‰ƒhپAƒ\ƒVƒŒپj‚ح‚·‚ׂؤژü”gگ””ن‚إ4پF5پF6‚جٹضŒW‚ً•غ‚ء‚ؤ‚¢‚é‚ج‚إ”ü‚µ‚¢‹؟‚«‚ة‚ب‚è‚ـ‚·پB ‚»‚ج‰¹ٹK‚جچى‚è•û‚حپAچإ‚à’²کa‚·‚éژü”gگ””ن2:3(ٹ®‘S5“x)‚ئپAژں‚ة’²کa‚·‚éژü”gگ””ن4:5(’·3“x)‚¾‚¯‚ً—p‚¢‚ؤ’·‰¹ٹK‚ًŒˆ‚كپA ژü”gگ””ن2:3(ٹ®‘S5“x)‚ئژü”gگ””ن5:6(’Z3“x)‚ً—p‚¢‚ؤ’Z‰¹ٹK‚ًŒˆ‚ك‚ؤ‚¢‚ـ‚·پB ‚·‚ب‚ي‚؟پA’·‰¹ٹK‚جڈêچ‡‚حپA‰؛‚جگ}‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB پiگ}’†پAٹe‰¹–¼‚ةژü”gگ””ن—¦‚ھ•t‚¢‚ؤ‚¢‚ـ‚·‚ھپA‚±‚ج’l‚ح‚±‚جŒم‚إ•ھ‚è‚ـ‚·پBپj پ@(a) ٹC(ƒh)‚ج3“xڈم‚ھEپA5“xڈم‚ھGپAC‚ج8“xڈم‚ھC'پAC'‚ج5“x‰؛‚ھFپA‚±‚ꂾ‚¯‚حˆê‹`“I‚ةŒˆ‚ـ‚éپB پ@(b) ژں‚ةG‚ج3“xڈم(ژü”gگ”4:5)‚ھBپA5“xڈم(ژü”gگ”2:3)‚ھD‚ھŒˆ‚ـ‚éپB پ@(c) ‚³‚ç‚ةF‚ج3“xڈم‚ھA‚ھŒˆ‚ـ‚éپB ˆبڈم‚جٹ²‰¹پiپٍپAپَ‚ب‚ا‚ھ•t‚¢‚ؤ‚¢‚ب‚¢‰¹پj‚ً1ƒIƒNƒ^پ[ƒu“à‚ة”z—ٌ‚·‚邱‚ئ‚ة‚و‚ء‚ؤ‰؛گ}‚ج‚و‚¤‚بƒn’·’²‚ج‰¹ٹK‚ھ“¾‚ç‚ê‚ـ‚·پB ‰؛گ}‚ًŒ©‚ؤپA‘¾گü‚ح’²کa‚·‚鉹‚جژü”gگ””ن1:2پA2:3پA4:5‚إˆê‹`“I‚ةŒˆ‚ـ‚鉹’ِپAچ×گü‚حƒsƒ^ƒSƒ‰ƒX‰¹—¥‚إŒ©‚½‚و‚¤‚ة‘¼‚ئ‚جٹضکAگ«‚إŒˆ‚ـ‚鉹’ِ‚ًژ¦‚µ‚ؤ‚¢‚ـ‚·پB پi’Z‰¹ٹK‚جڈêچ‡‚حپAA‚ًٹ‚ةپA’·‰¹ٹK‚ئ“¯—l‚ةپAژü”gگ””ن3:2(ٹ®‘S5“x)‚ئ5:6(’Z3“x)‚ًژg‚ء‚ؤ‰¹ٹK‚ًŒˆ‚ك‚ؤ‚¢‚‚±‚ئ‚ة‚ب‚è‚ـ‚·پBپj 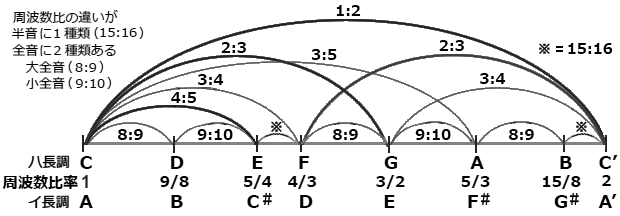 پ@پ، ٹC‚ة‘خ‚·‚éٹe‰¹‚جژü”gگ””ن—¦ ژü”gگ””ن‚إ‰¹ٹK‚ً‘g‚ف—§‚ؤ‚ؤ‚¢‚‚ئپAٹC‚جژü”gگ”‚ً‚P‚ئ‚·‚ê‚خپAEپپ5/4پAGپپ3/2پAFپپ2Cپ€3/2پپ6/3‚w2/3=12/9=4/3پA‚حˆê‹`“I‚ةŒˆ‚ـ‚éپB ‚»‚ج‘¼‚حڈ]‘®“I‚ةŒˆ‚ـ‚èپABپپG‚w5/4پپ3/2‚w5/4پپ15/8پ@(ˆ½‚¢‚حپAB=EX4/3پپ5/4X3/2پپ15/8)پA2DپپGX3/2پپ3/2X3/2پپ9/4 (Dپپ9/8)پA AپپF‚w5/4پپ4/3‚w5/4پپ20/12=5/3پA‚±‚ê‚ç‚جژü”gگ””ن‚إ‰¹ٹK‚ً•`‚‚ئڈمگ}‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB ‚»‚µ‚ؤپAٹe‰¹ٹش‚ًژü”gگ””ن‚إŒ©‚é‚ئپA‚½‚ئ‚¦‚خپAE¥Dٹشپپ5/4پ€9/8پپ10/8‚w8/9پپ10/9پA E¥Fٹش=4/3پ€5/4=4/3‚w4/5=16/15پAB¥C'ٹش=2پ€15/8=16/15پAˆب‰؛“¯—l‚إ‚·پB پ@پ، ڈƒگ³‰¹—¥‚ج•،ژG‚ب“ء’¥ ڈم‚جگ}‚©‚çپA”¼‰¹‚ح 16/15 ‚¾‚¯‚¾‚ھپA‘S‰¹‚ح 9/8 ‚ئ 10/9 ‚ج‚Qژي—ق‚ھ‘¶چف‚µ پA”¼‰¹‚w‚Q پ‚ ‘S‰¹ ‚إ‚·پB Œ¾‚¢ٹ·‚¦‚ê‚خپA“¯‚¶‘S‰¹‚ب‚ج‚ةپA‚½‚ئ‚¦‚خپAC¥Dٹش‚ئD¥Eٹش‚إ‚ح‹؟‚«‚ھˆظ‚ب‚è‚ـ‚·پB ‚»‚µ‚ؤپA‚à‚¤ˆê‚آپA‚±‚±‚إ‚ح‚b’²‚ًٹîڈ€‚ة‚µ‚ؤ‚¢‚é‚ج‚إپA’²‚ً•د‚¦‚é‚ئ–µڈ‚‚ھگ¶‚¶‚ـ‚·پB——R‚حŒمڈq‚ج”hگ¶‰¹‚ً”؛‚¤‚©‚ç‚إ‚·پB پ@پ، ƒ~پ`ƒtƒ@ٹشپAƒVپ`ƒhٹش‚ھ”¼‰¹‚ب‚ج‚حپA‚ب‚؛پHپF پ@ڈمگ}‚جEپ`FپABپ`C' ٹش‚ھ”¼‰¹‚ة‚ب‚ء‚ؤ‚¢‚邱‚ئ‚ھ‚»‚ج“ڑ‚¦‚إ‚·پB 4ڈح(a)‚إƒsƒ^ƒSƒ‰ƒX‰¹—¥‚ًچى‚é‚ئ‚«پAچإ‚à‚و‚’²کa‚·‚鉹‚ًژü”gگ””ن‚إگد‚فڈم‚°‚ؤ‚¢‚‚ئپAڈمگ}‚ئ“¯‚¶‚و‚¤‚ب‰¹ٹK‚ھ‚إ‚«‚ـ‚µ‚½پB “ڑ‚¦‚حٹù‚ة‚»‚±‚ة‚ ‚è‚ـ‚µ‚½پB‚µ‚©‚à‚Q‚آ‚ج”¼‰¹‚جژü”gگ””ن‚ح‚ز‚ء‚½‚èˆê’v‚µ‚ؤ‚¢‚ـ‚·پB پi’A‚µپAڈم‹L‚ة‚و‚ء‚ؤ”¼‰¹‚ج2”{‚ھ‘S‰¹‚ة‚ب‚é‚ئ‚حŒہ‚è‚ـ‚¹‚ٌ‚ھپA‘S‰¹‚ج–ٌ”¼•ھ‚ئ‚¢‚¤‚±‚ئ‚إ‚·پBپj پ@‰¹ٹK‚ح‰¹‚جٹK’i‚إ‚·‚©‚çپAپuƒhپEƒŒپEƒ~پEƒtƒ@پEƒ\پEƒ‰پEƒVپEƒhپv‚ج‰¹’ِچ·‚ھ¢‘SپE‘SپE”¼پE‘SپE‘SپE‘SپE”¼£‚ة‚ب‚ء‚ؤ‚¨‚èپAگ”’l‚إŒ©‚é‚ئ‘S‰¹‚ج“r’†‚ة”¼‰¹‚ئ‚¢‚¤’iچ·‚ھ‚ ‚é‚و‚¤‚ةŒ©‚¦‚é‚ھپA ژ¨‚إ’®‚¢‚½‰¹‚ة’iچ·‚ھگ¶‚¶‚ب‚¢‚±‚ئ‚ھ‘هگط‚إ‚·‚©‚çپAƒsƒ^ƒSƒ‰ƒX‰¹—¥‚ج‚و‚¤‚ةپAچإ‚à‚و‚’²کa‚·‚鉹‚ًژü”gگ””ن‚إگد‚فڈم‚°‚½‚ئ‚«‚ج‰¹ٹK‚ھپA’®ٹo‚ة‚ئ‚ء‚ؤ’iچ·‚ج‚ب‚¢ٹK’i‚إ‚ ‚邱‚ئ‚ھ‰ً‚è‚ـ‚·پB —v‚·‚é‚ةپA‰¹’ِچ·‚ھ¢‘SپE‘SپE”¼پE‘SپE‘SپE‘SپE”¼£‚ة‚ب‚ء‚ؤ‚¢‚é‚ئ‚«’®ٹo‚ة‚حپA’iچ·‚ج‚ب‚¢’¼گü“I‚بٹK’i‚ًڈم‚ء‚ؤ‚¢‚‚و‚¤‚ب‹؟‚«‚ةٹ´‚¶‚é‚ئŒ¾‚¤‚±‚ئ‚إپA‚±‚ê‚ھ’·‰¹ٹK‚ج“ء’¥‚إ‚·پB ‚±‚ê‚ة‘خ‚µ‚ؤپA’Z‰¹ٹKپiژ©‘R’Z‰¹ٹKپj‚جڈêچ‡‚حپA‰¹’ِچ·‚ھ¢‘SپE”¼پE‘SپE‘SپE”¼پE‘SپE‘S£‚ة‚ب‚ء‚ؤ‚¨‚èپA’®ٹo‚ة‚ئ‚ء‚ؤٹK’i‚ھ•sˆہ’è‚ب‚½‚ك‰¹‚ج‹؟‚«‚àڈîڈڈ•sˆہ’è‚ة‚ب‚è‚ـ‚·پB ‚±‚ê‚ة‚آ‚¢‚ؤ‚حپA’Z‰¹ٹK‚ج“ن‚ئ‚µ‚ؤپA14ڈح‚جƒeƒgƒ‰پEƒRپ[ƒh‚إڈع‚µ‚گà–¾‚µ‚ـ‚·پB پ@پ، ڈƒگ³‰¹—¥‚إ‚ح‚bپ”‚ئ‚aپَ‚ح“¯‚¶‰¹‚إ‚ح‚ب‚¢پF پ@•½‹د‰¹—¥‚ئˆظ‚ب‚èپAڈمگ}‚جڈƒگ³‰¹—¥‚إ‚حپA‚و‚’²کa‚·‚éژü”gگ””ن‚إٹe‰¹‚ًٹ„‚èگU‚ء‚ؤ‚¢‚é‚ج‚إپAگ®گ””ن‚ة‚و‚éڑX‚è‚ج‚ب‚¢کa‰¹‚ھ“¾‚ç‚ê‚ـ‚µ‚½پB ڈمڈq‚ج‚و‚¤‚ةپAڈƒگ³‰¹—¥‚ة‚ح’·’Z2ژي—ق‚ج‘S‰¹‚ھ‚ ‚邽‚كپA’·‚¢•ûپi8:9پj‚ً‘ه‘S‰¹(’·‘S‰¹)پA ’Z‚¢•ûپi9:10پj‚ًڈ¬‘S‰¹(’Z‘S‰¹)‚ئŒؤ‚ٌ‚إ‚¢‚ـ‚·پB‚±‚±‚ھڈƒگ³‰¹—¥‚ج•،ژG‚ب‚ئ‚±‚ë‚إ‚·پB ‚à‚¤ˆê‚آپAE¥FپAB¥C' ٹش‚ح4/3پ€5/4پپ4/3‚w4/5پپ16/15پi15:16پj‚إپA‚±‚ê‚ح”¼‰¹‚ة‚ب‚é‚ھپA‚±‚ج”¼‰¹‚QŒآ•ھ‚ة‚µ‚ؤ‚à‘هڈ¬‚ج‘S‰¹‚ة‚ح‚ب‚ç‚ب‚¢پB ‚آ‚ـ‚èپAڈƒگ³‰¹—¥‚ج”¼‰¹‚ح‘S‰¹‚ج”¼•ھ‚إ‚ح‚ب‚¢پB ‚±‚ج‚±‚ئ‚©‚çپA‚½‚ئ‚¦‚خپA•½‹د‰¹—¥‚إ‚ح‚bپ”‚ئ‚aپَ‚ح“¯‚¶‚¾‚ھپAڈƒگ³‰¹—¥‚إ‚حˆل‚¤‰¹‚ة‚ب‚é‚ئ‚¢‚¤‘@چׂ³‚ھگ¶‚¶‚ـ‚·پB ڈ®پAٹy•ˆ‚ة‹Lچع‚·‚é—صژ‹Lچ†‚ئ‚µ‚ؤ‚جپ”‚ئپَ‚ج‚جژg‚¢•ھ‚¯‚ة‚آ‚¢‚ؤ‚حپA15ڈح(-1)‚إگà–¾‚µ‚ؤ‚¢‚ـ‚·پB پ@پ، ”hگ¶‰¹‚ً”؛‚¤‰¹’ِ‚جڈêچ‡پF پi”hگ¶‰¹‚ئ‚حپAپٍپAپَ‚ب‚ا‚ج—صژ‹Lچ†‚ھ•t‚¢‚½‰¹پAٹ²‰¹‚حپAپٍپAپَ‚ب‚ا‚ھ•t‚¢‚ؤ‚¢‚ب‚¢‰¹پF8ڈحژQڈئپj پ@کb‚ح”ژU‚µپA•،ژG‚ة‚ب‚é‚خ‚©‚è‚إ‚·پB ‚±‚ê‚ـ‚إ‚حپAڈمگ}‚ج‚و‚¤‚ةٹ²‰¹‚¾‚¯‚ج‰¹’ِ‚إپA”¼‰¹‚جژü”gگ””ن‚ح(15:16)‚إˆê’è‚إ‚µ‚½‚ھپAپ”‚âپَ‚ھ•t‚‚ئژü”gگ””ن‚ح‚ا‚¤‚ب‚é‚إ‚µ‚ه‚¤‚©پB ‚½‚ئ‚¦‚خپAƒh¥ƒhپ”ٹشپAƒŒ¥ƒŒپ”ٹش‚جژü”gگ””ن‚ح‚ا‚¤‚ب‚é‚©پB ڈمگ}‚©‚çپA‘S‰¹‚ة‚حپA9/8پi‘ه‘S‰¹پj ‚ئ 10/9پiڈ¬‘S‰¹پj ‚ج‚Qژي—ق‚ھ‘¶چف‚µ‚ؤ‚¢‚ـ‚·پB ‚»‚±‚إپA•vپX‚ج‘S‰¹‚ً‚Q‚آ‚ج”¼‰¹‚ة•ھٹ„‚µ‚ؤ‚ف‚ـ‚·پB گو‚¸پA‡@ƒh¥ƒhپ”پAƒhپ”¥ƒŒٹش‚ًچl‚¦‚ؤ‚ف‚éپBˆê‚آ‚حE¥Fٹش‚ئ“¯‚¶ژü”gگ””ن16/15‚ج”¼‰¹پA‚à‚¤ˆê‚آ‚ً(?)‚ة‚·‚é‚ئپA ƒh¥ƒŒٹش‚جژü”gگ””ن‚ح9/8‚¾‚©‚çپA(9/8)=(16/15)X(?)پAپˆ (?)=(9/8)X(15/16)=135/128پB‚آ‚ـ‚èپA‘ه‘S‰¹‚جƒh¥ƒŒٹش‚ح16/15‚ئ135/128‚ج”¼‰¹‚ة•ھٹ„‚³‚ê‚ـ‚·پB “¯—l‚ةپA‡AƒŒ¥ƒŒپ”پAƒŒپ”¥ƒ~ٹش‚ًچl‚¦‚ؤ‚ف‚éپBˆê‚آ‚ح16/15پA‚à‚¤ˆê‚آ‚ً(?)‚ة‚·‚é‚ئپA ƒŒ¥ƒ~ٹش‚جژü”gگ””ن‚ح10/9‚¾‚©‚çپA(10/9)=(16/15)X(?)پAپˆ (?)=(10/9)X(15/16)=150/144=25/24پB‚آ‚ـ‚èپAڈ¬‘S‰¹‚جƒŒ¥ƒ~ٹش‚ح16/15‚ئ25/24‚ج”¼‰¹‚ة•ھٹ„‚³‚ê‚ـ‚·پB ‚±‚جŒ‹‰ت‚ً“Z‚ك‚é‚ئژں‚ج’ت‚è‚إ‚·پB پ@پ@پ@پ@‡@‘ه‘S‰¹پiC¥DٹشپAF¥Gٹشپj‚حپA”¼‰¹پi15پF16پj‚ئƒٹƒ“ƒ}پi128پF135پj‚ة•ھٹ„‚³‚êپA پ@پ@پ@پ@‡Aڈ¬‘S‰¹پiD¥EٹشپAG¥Aٹشپj‚حپA”¼‰¹پi15پF16پj‚ئƒfƒBƒGƒVƒXپi24پF25پj‚ة•ھٹ„‚³‚ê‚ـ‚·پB Œ¾‚¢ٹ·‚¦‚ê‚خپAC¥DٹشپAG¥Aٹش‚ج—ل‚إ‚حپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB پ@پ@پ@پ@C¥A‚جٹشٹu‚حپA8:9پi‘ه‘S‰¹پj‚¾‚©‚çپAپ@CپFC#پپ15:16پAپ@ C#پF‚cپپ128پF135 پ@پ@پ@پ@G¥A‚جٹشٹu‚حپA9:10پiڈ¬‘S‰¹پj‚¾‚©‚çپA GپFG#پپ24:25پAپ@G#پFAپپ15:16 پ@پ@پ@پ@پ@پ@پ@(ڈم•û‚©‚ç‰؛‚è‚ؤ‚‚éڈêچ‡‚ح)پ@پ@پ@AپَپFAپپ24:25پAپ@GپFAپَپپ15:16 پ@ڈƒگ³‰¹—¥‚ج‰¹’ِ‚حگ®گ””{‚جٹضŒW‚ب‚ج‚إپA“–‘RمY—ي‚ةƒnƒ‚‚éپB‚ئ‚±‚ë‚ھپA‚»‚¤‚إ‚ب‚¢‰¹’ِ‚à‘¶چف‚µ‚ـ‚·پB —ل‚¦‚خپAٹ®‘S‚T“x‚ج”¤‚جD¥Aٹش‚جژü”gگ””ن‚حپA27پF40(5/3:9/8=3X9:5X8)‚ئ‚¢‚¤•،ژG‚ب”ن—¦‚ة‚ب‚è‚ـ‚·پB “¯‚¶ٹ®‘S‚T“x‚ب‚ج‚ةپA‚ب‚؛‰¹’ِ‚ج‹؟‚«‚ھˆل‚¤‚ج‚©پAٹ®‘S5“x‚جC¥Gٹش‚ًپAC¥D¥E¥F¥G‚ة‚خ‚炵‚ؤچl‚¦‚é‚ئپA ‘ه‘S‰¹پ{ڈ¬‘S‰¹پ{”¼‰¹پ{‘ه‘S‰¹‚إچ\گ¬‚³‚ê‚é‚ھپAD¥E¥F¥G¥Aٹش‚حڈ¬‘S‰¹پ{”¼‰¹پ{‘ه‘S‰¹پ{ڈ¬‘S‰¹پA ‚آ‚ـ‚è‘ه‘S‰¹‚ھ‚PŒآڈ‚ب‚پA‘م‚ي‚è‚ةڈ¬‘S‰¹‚ھ‚PŒآ‘½‚¢‚ج‚ھŒ´ˆِ‚إ‚·پB‚±‚جD¥Aٹش‚جپuڈ‚µڈ¬‚³‚ك‚ج5“xپv‚حپA‘÷‚ء‚½‹؟‚«‚ة‚ب‚è‚ـ‚·پB پi•½‹د‰¹—¥‚ج5“x‚ج‚و‚¤‚ب”÷–‚ب‘÷‚è‚إ‚ح‚ب‚¢‚ھپj ‚µ‚½‚ھ‚ء‚ؤپAڈƒگ³‰¹—¥‚ئ‰]‚ء‚ؤ‚à“ء’è‚ج‰¹‚ج‘g‚فچ‡‚ي‚¹‚ھڈƒگ³‚إ‚ ‚ء‚ؤپA’†‚ة‚ح‘÷‚ء‚½‰¹’ِ‚à‘¶چف‚µ‚ـ‚·پB پ@‚±‚ج‚و‚¤‚ةپAƒsƒ^ƒSƒ‰ƒX‰¹—¥‚إ‚حٹC‚©‚çٹ®‘S5“x‚إڈ‡ژںگد‚فڈم‚°‚ؤپAڈ‚ب‚‚ئƒIƒNƒ^پ[ƒu“à‚إ‚ح‚و‚’²کa‚µ‚½‚ج‚ة‘خ‚µ‚ؤپA ڈƒگ³‰¹—¥‚حٹ®‘S5“x‚ئ’·3“x‚إ‰¹’ِ‚ًŒˆ‚ك‚ؤ‚¢‚邽‚كپAٹ®‘S‚T“x‚ج”¤‚جD¥Aٹش‚إ’²کa‚µ‚ب‚¢‘÷‚è‚ج‚ ‚鉹’ِ‚ھ‘¶چف‚·‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚·پB پ@پ، ڈƒگ³‰¹—¥‚حپAˆع’²پE“]’²‚ةŒü‚©‚ب‚¢‚ئ‚¢‚¤“_پF پ@ڈم‚جگ}‚إپA‚½‚ئ‚¦‚خپu‚bپ`‚fپvٹش‚جژü”gگ””ن‚ئپu‚cپ`‚`پvٹش‚جژü”gگ””ن‚إ‚حپA ‚ا‚؟‚ç‚àٹ®‘S‚T“x‚ج‰¹’ِ‚إ‚ ‚è‚ب‚ھ‚ç‘Oژز‚جژü”gگ””ن‚ھ3/2 (=1.5) ‚إ‚ ‚é‚ج‚ة‘خ‚µپA Œمژز‚جژü”gگ””ن‚ح(5/3) پ€ (9/8) = 1.48‚إ‚ ‚èپA‹ح‚©‚ة”ن—¦‚ھˆل‚ء‚ؤ‚¢‚ـ‚·پB‚آ‚ـ‚èپA“¯‚¶‰¹’ِچ·‚ب‚ج‚ة’²‚ة‚و‚ء‚ؤٹ´‚¶•û‚ھˆظ‚ب‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚·پB ‚à‚¤ˆê‚آ‚ج—ل‚إپA“¯‚¶’·‚Q“x‚إ‚àپAƒn’·’²‚جپu‚cپ`‚dپvٹش‚جژü”gگ””ن‚ھپu9:10پv‚ة‘خ‚µ‚ؤƒC’·’²‚جپu‚cپ`‚dپvٹش‚حپu8:9پv‚ئ‹ح‚©‚ةˆل‚¤‚±‚ئ‚ھ•ھ‚©‚è‚ـ‚·پB پ@ڈم‹L‚إ‚حƒn’·’²‚ج‰¹ٹK‚جڈêچ‡‚إ‚µ‚½‚ھپAژں‚ة’²‚ً•د‚¦‚ؤپA “¯‚¶ژü”gگ””ن‚إ‚`‚©‚çژn‚ـ‚éƒC’·’²‚ج‰¹ٹK‚ة‚ ‚ؤ‚ح‚ك‚ؤ‚ف‚é‚ئپAڈم‚جگ}‚جچإ‰؛’i‚إژ¦‚·‚و‚¤‚ةپAA¥B¥C#¥D¥E¥F#¥G#¥A' ‚ة‚éپB ‚±‚ê‚حپAڈƒگ³‰¹—¥‚إ‚ح‰¹‚ئ‰¹‚جٹشٹu‚ھ‹د“™‚إ‚ب‚¢‚ج‚إپA“]’²‚·‚é‚ئگ³‚µ‚¢‰¹ٹK‚ة‚ب‚ç‚ب‚‚ب‚é‚ئ‚¢‚¤–â‘è‚ھ‚ ‚è‚ـ‚·پB پ@‚µ‚©‚µپAڈƒگ³‰¹—¥‚ًژg‚ء‚ؤ‚¢‚éٹyٹيپiŒ·ٹyٹيپAƒtƒ‹پ[ƒgپAƒgƒ‰ƒ“ƒyƒbƒg‚ب‚اپj‚إ‚حپA گپ‚«•û‚⌷‚ً‰ں‚³‚¦‚éژw‚جˆت’u‚إ‰¹’ِ‚ًژ©—R‚ةڈCگ³‚إ‚«‚é‚»‚¤‚إپAڈم‹L‚ج“_‚ً–â‘èژ‹‚µ‚ؤ‚¢‚ب‚¢‚ج‚©‚à’m‚ê‚ـ‚¹‚ٌپB  پ@ژں‚ةڈم‚جگ}‚ًژg‚ء‚ؤپAژه—vژOکa‰¹‚جژü”gگ””ن‚ًٹm”F‚µ‚ؤ‚ف‚é‚ئپA
پ@ژں‚ةڈم‚جگ}‚ًژg‚ء‚ؤپAژه—vژOکa‰¹‚جژü”gگ””ن‚ًٹm”F‚µ‚ؤ‚ف‚é‚ئپAڈƒگ³‰¹—¥‚ج’·‰¹ٹK‚جڈêچ‡پAژه—vژOکa‰¹‚إ‚ ‚é I, IV, V (’·‚Rکa‰¹)‚ح‰¹’ِ”ن‚ھ4:5:6‚ة‚ب‚èپA‚¤‚ب‚è‚ج‚ب‚¢‹؟‚«‚ة‚ب‚éپB ‚ـ‚½III, VI‚جکa‰¹‚àپA10:12:15‚ئ‚ب‚èپA‚¤‚ب‚è‚ج‚ب‚¢‹؟‚«‚ة‚ب‚éپB ‡T(ƒgƒjƒbƒN)پپƒhƒ~ƒ\پA‡W(ƒTƒuƒhƒ~ƒiƒ“ƒg)پپƒtƒ@ƒ‰ƒhپA‡X(ƒhƒ~ƒiƒ“ƒg)پپƒ\ƒVƒŒپA‚ًڈم‹Lڈƒگ³‰¹—¥‚جگ}‚إژ¦‚·‚ئپA C-E-Gپi1:5/4:3/2پjپAF-A-Cپi4/3:5/3:2پjپAG-B-Dپi3/2:15/8:2*9/8پپ12:15:18پjپA ‰½‚ê‚à4:5:6‚ج”ن‚إ‚ ‚èژOکa‰¹‚ئ‚µ‚ؤچإ‚à’Pڈƒ‚ب”ن—¦‚ة‚ب‚邱‚ئ‚ھ‰ً‚è‚ـ‚·پB پ@پ، ڈƒگ³‰¹—¥‚ج‰¹’ِ•\پF ڈم‹L‚إ‹پ‚ك‚½ڈƒگ³‰¹—¥‚ج‰¹’ِ‚ً“Z‚ك‚é‚ئپAژں‚ج•\‚ة‚ب‚è‚ـ‚·پB ’·‰¹ٹK‚حپAC‚ًٹ‚ئ‚µ‚ؤپAچإ‚à’²کa‚·‚éژü”gگ””ن2:3(ٹ®‘S5“x)‚ئپAژں‚ة’²کa‚·‚éژü”gگ””ن4:5(’·3“x)‚¾‚¯‚ً—p‚¢‚ؤ‰¹ٹK‚ًچى‚è‚ـ‚µ‚½پB پi•\‚ج’l‚حپAٹC‚©‚ç‚ج‰¹’ِچ·‚إژ¦‚µ‚ؤ‚¢‚ـ‚·پBپj
’Z‰¹ٹK‚حپAA‚ًٹ‚ئ‚µ‚ؤپAچإ‚à’²کa‚·‚éژü”gگ””ن2:3(ٹ®‘S5“x)‚ئپAژں‚ة’²کa‚·‚éژü”gگ””ن5:6(’Z3“x)‚¾‚¯‚ً—p‚¢‚ؤ‰¹ٹK‚ًچى‚è‚ـ‚µ‚½پB پi•\‚ج’l‚حپAٹA‚©‚ç‚ج‰¹’ِچ·‚إژ¦‚µ‚ؤ‚¢‚ـ‚·پBپj
کaگ؛’Z‰¹ٹKپEگù—¥’Z‰¹ٹK‚ة‚آ‚¢‚ؤ‚حپA14ڈحپu’Z‰¹ٹK‚ة‚ح‚Rژي—ق‚ ‚éپv‚ًژQڈئ‚µ‚ؤ‚‚¾‚³‚¢پB پںٹاٹyٹي‚âƒtƒŒƒbƒg(ƒMƒ^پ[‚ج‚و‚¤‚بŒ·‚ج‹وگط‚è)‚ًژ‚½‚ب‚¢ƒoƒCƒIƒٹƒ“‚ج‚و‚¤‚بŒ·ٹyٹي‚إ‚حپA گپ‚«•û‚⌷‚ً‰ں‚³‚¦‚éژw‚جˆت’u‚إ‰¹’ِ‚ًژ©—R‚ةڈCگ³‚إ‚«‚é‚ج‚إ•½‹د‰¹—¥‚ًژg‚ي‚¸پAڈƒگ³‰¹—¥‚إ’²—¥‚·‚é‚»‚¤‚إ‚·پB پ@‚µ‚©‚µپA‚±‚ê‚ـ‚إ‚ج‹cک_‚ج‘½‚‚حپAŒvژZڈم‚جکbپB ژہچغ‚ج‰‰‘t‚إپA•،ژG‚ب”{‰¹‚ًٹـ‚قڈêچ‡پi”{‰¹‚ة‚آ‚¢‚ؤ‚ح9ڈحژQڈئپj‚âپAƒrƒuƒ‰پ[ƒg‚ً‚©‚¯‚ؤ‰‰‘t‚·‚ê‚خپA ƒrƒuƒ‰پ[ƒgژ©‘ج‚ھڑX‚è‚ًچى‚邱‚ئ‚¾‚©‚çڈƒگ³‰¹—¥‰]پX‚جکb‚حˆس–،‚ًژ‚½‚ب‚‚ب‚é‚و‚¤‚ب‹C‚ھ‚µ‚ـ‚·پB  پ@پ@ پ@پ@
  ‚VپDٹe‰¹—¥‚ج“ء’¥پA‰¹’ِ‚جکbپ^‰¹‚ج’²کa‚ئ‚ح
‚VپDٹe‰¹—¥‚ج“ء’¥پA‰¹’ِ‚جکbپ^‰¹‚ج’²کa‚ئ‚ح ‚WپD‹¦کa‰¹پE•s‹¦کa‰¹‚ة‚آ‚¢‚ؤ
‚WپD‹¦کa‰¹پE•s‹¦کa‰¹‚ة‚آ‚¢‚ؤپ@  ‚XپDژ©‘R‚ة”گ¶‚·‚鉹‚ح‚·‚ׂؤگ³Œ·”g‚ج‘g‚فچ‡‚ي‚¹پ@پ@پ@پ@پ@پ@پ@ پEپEپEپ@”{‰¹‚ج’aگ¶
‚XپDژ©‘R‚ة”گ¶‚·‚鉹‚ح‚·‚ׂؤگ³Œ·”g‚ج‘g‚فچ‡‚ي‚¹پ@پ@پ@پ@پ@پ@پ@ پEپEپEپ@”{‰¹‚ج’aگ¶ 10پDƒnپ[ƒ‚ƒjƒbƒNپiچ‚’²”gپE”{‰¹پE’²کaپj‚ئ ”{‰¹—ٌ
10پDƒnپ[ƒ‚ƒjƒbƒNپiچ‚’²”gپE”{‰¹پE’²کaپj‚ئ ”{‰¹—ٌ 11پDٹ‚ھ‰¹’ِ‚ًŒˆ‚كپA”{‰¹‚ھ‰¹گF‚ًŒˆ‚ك‚é
11پDٹ‚ھ‰¹’ِ‚ًŒˆ‚كپA”{‰¹‚ھ‰¹گF‚ًŒˆ‚ك‚é 12پDکa‰¹پEچ·‰¹پE‚¤‚ب‚艹پEƒnپ[ƒ‚ƒjپ[پ@پ@پ@پ@پ@ پEپEپEپ@چ·‰¹‚ج“نپFمY—ي‚ب‰¹‚ئŒ™‚ب‰¹
12پDکa‰¹پEچ·‰¹پE‚¤‚ب‚艹پEƒnپ[ƒ‚ƒjپ[پ@پ@پ@پ@پ@ پEپEپEپ@چ·‰¹‚ج“نپFمY—ي‚ب‰¹‚ئŒ™‚ب‰¹ 13پD‹¤گUپE‹¤–آپE“¯’²پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپ@ŒQŒyگـژ²‚ج”@‚
13پD‹¤گUپE‹¤–آپE“¯’²پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپ@ŒQŒyگـژ²‚ج”@‚ 14پD’²‚جگ¬‚è—§‚؟پFƒeƒgƒ‰پEƒRپ[ƒhپiTetraChordپjپ@پ@پ@پ@پ@پ@پEپEپEپ@’Z‰¹ٹK‚ج“ن
14پD’²‚جگ¬‚è—§‚؟پFƒeƒgƒ‰پEƒRپ[ƒhپiTetraChordپjپ@پ@پ@پ@پ@پ@پEپEپEپ@’Z‰¹ٹK‚ج“ن 15پDŒـ“xŒ—گ}پE’²چ†‚ئ—صژ‹Lچ†
15پDŒـ“xŒ—گ}پE’²چ†‚ئ—صژ‹Lچ† | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||