 (���̉��y) |
�@���y�̌��_��T�� |
�摜���H�L�� �V�v�w�̗��L�^ |
 �P�D�w �i
�P�D�w �i�@���i�̉�b�œ�����O�̂悤�ɔ�ь������t�̒��ɂ�����Ȃ����Ƃ���R����B���K���ł����w�i�́H�A���������F�Ƃ́H�A���F�����߂�{���̐��̂́H�A�n�[���j�[�̐��̂́H�A �y�����^�߂��������Ƃ́H�A�y�Ȃ̎d�g�݂́H�A���X�A�S���Ƃ͑�R����A���������R���ۂ̒�����w�ڂ��Ƃ����B �@�l�́A�{�\�̂܂܂ɉ��y�Ƃ̌q�����z���Ă����B�Ȃ�Ή��y�͐l�דI�ɍl����ꂽ���ł͂Ȃ��A���R���ۂ̒����琶�܂ꂽ���ۂ��낤�Ɛ��@�ł���B ���Ƃ��A�T�x�̒��a�A�{����̋����A�����̃n�[���j�[�A�K���I���Y���̒��̕s�K���ȗh�炬�A�ȂǁA���y�̌��_�����R�@���̒��ɂ���B ���̎��R�@���Ƃ����͎̂��ɍ����I�ɏo���Ă���A�����Z�������Z�̔��ӎ��̕����������Ɋ����B �����l����ƁA���y���肫�ő��ԓI�Ɋw�Ԃ��A�g�߂Ȏ��R���ۂ̒����特�y���w�����A�������[�܂邱�Ƃ����������B �����ŁA����܂Œf�ГI�ɓ������y�̒m�����A���K�Ɛ��������˂Ĕ��Y�^�̂���œZ�߂Ă݂܂����B  �Q�D���R���ۂ̒����特�y���w�ԂƗ������₷���@�@�@�@�@�@�@�E�E�E�@���y�Ɛl�̖{�\
�Q�D���R���ۂ̒����特�y���w�ԂƗ������₷���@�@�@�@�@�@�@�E�E�E�@���y�Ɛl�̖{�\ �R�D�a�މ��ɂ́A�s�K���ȗh�炬�������@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@Simple is Best
�R�D�a�މ��ɂ́A�s�K���ȗh�炬�������@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@Simple is Best �S�D�b�艮�̓S�ł����特�y�̑��݂�\�z
�S�D�b�艮�̓S�ł����特�y�̑��݂�\�z�@���j�̏o���_�ɒH�蒅���Ă݂�A���y�̗���������ȂɊȒP�������̂��B ����܂ł́A���K�̐��藧������m�炸�A�l�������Ƃ��Ȃ��������A�������Ă݂�Ɗy���̌����ɂ������L��������������܂��B �@�́A������2,500�N���O�A�M���V���̓N�w�҂Ő��w�҂ł��������s�^�S���X(�I���O582�`497�N)������̉����Ȋw�I�ɉ𖾂��A �����͐U�����̔�ŕ\��������Ƃ������B ���̔����ɂ͊���̈�b�����邪�A���̒��Œb�艮����̗Ⴊ����₷���B ������A�b�艮����̑O��ʂ肩�������Ƃ��A���l�̐E�l�����Ƃ�U����ēS�ł����Ă��邤���ɁA����I�A�Ǝv�������Ƃ�����B ���ƂœS��ł��̒��ɂ́A����̉����d�Ȃ����Ƃ��A�S�n�悭�����ꍇ�ƁA�����łȂ��ꍇ�����邱�ƂɋC�t�����B���ꂪ���̒��a�̔����ł��B ���Ƃׂ�ƁA�d���̔䂪�u3:2�v�̂Ƃ��ɖ鉹���悭���a�������ƂɋC�Â����B �X�ɁA�d����2:1�̂Ƃ��A4:3�̂Ƃ����悭���a���邱�ƂɋC�Â����B 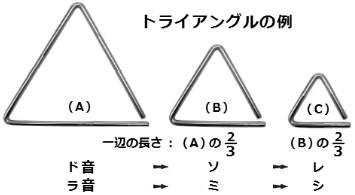 �@���Ƃ̑���ɁA���t��ł悭��������y��g���C�A���O���ł݂�Ƃ����ƕ�����₷���B ����͋����̖_���A�O�p�`�ɋȂ����`��̊y��ŁA�}�̂悤�ɂR�̃g���C�A���O��(�`)(�a)(�b)��p�ӂ��A(�a)�͈�ӂ̒�����(�`)��3����2�A(�b)��(�a)��3����2�Ƃ��܂��B ���̂����A�Q���ɖ炵���Ƃ�(�`)��(�a)�A(�a)��(�b)�̉��͂悭���a���A(�`)��(�b)�͒��a���Ȃ����Ƃ�����܂����B ����5�͂ʼn��邱�Ƃł����A������(�`)���h���Ȃ�(�a)�̓\���A(�a)���\���Ȃ�(�b)�̓�������͂��ł��B �܂�A��ӂ̒������Z���Ȃ�������ɂȂ�̂ŁA(�`)�Ńh����A(�a)�̎��g����(�`)��3/2�{�Ń\���A (�b)��(�a)��3/2�{�̃����A���Ȃ킿(�`)��9/4=2X(9/8)��1�I�N�^�[�u���9/8�{�̃����ɂȂ�B ���̎�������ɁA���K�̑��݂�˂��~�߂Ă������ƂɂȂ邪�A������e�Ղɂ��邽�߁A�s�^�S���X�͋��Ƃ̑���Ɍ��̒����̔�ɒu�������āA���ڂ������K�̊m���ւƔ��W�����Ă����܂����B �ł́A�Ȃ�(�`)���h���Ȃ�A�ӂ̒�����2/3��(�a)���\���A�����(�b)�������ɂȂ�̂��A���̎��_�ł͂܂��������܂���B 5�͂Ŏ��ۂɃs�^�S���X����������Ă݂�Ɨ����ł��܂��B �@(��) �s�^�S���X�̎��� �F ���a���鉹�ƌ��̒����̔�̊W��T�� 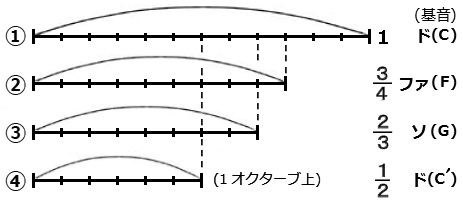 �@��L�g���C�A���O���̑���ɁA�E�}�̂悤�ȁA�����P�̌��ƁA����3/4�A2/3�A�����̌���p�������Ƃ��A
���̒����ɂ���ĉ��̍������ς��A���A�@�`�C�Ɏ����䗦�̌����o�����݂͌��ɒ��a���邱�Ƃ��m�F�����B
�@��L�g���C�A���O���̑���ɁA�E�}�̂悤�ȁA�����P�̌��ƁA����3/4�A2/3�A�����̌���p�������Ƃ��A
���̒����ɂ���ĉ��̍������ς��A���A�@�`�C�Ɏ����䗦�̌����o�����݂͌��ɒ��a���邱�Ƃ��m�F�����B�@�����P�̌��̊���h(�b)�ɂ���A�A����3/4�̌��̉��̓t�@(�e)�̉��A�B����2/3�̌��̉��̓\(�f)�A �C�����������̌��̉��͂P�I�N�^�[�u�����h(�b�f)�ɂȂ�A �v�X�̉��́A��b(�h)�Ƃ悭���a���邱�Ƃ��������̂ł��B �����ł͌��̒����ɑ��鉹�K�̈��������������ł����A�u�h���~�t�@�\���V�h�v�̂ł���ߒ���5�͂̃s�^�S���X�����ŏڂ����������܂��B �@��}�Ŋ�̌��̒����@��12���������̂́A���̒���3:2�A����сA4:3�̉��͊�ɑ��Ă悭���a���邱�Ƃ�O��ɂ���ƁA �P�I�N�^�[�u��12(=3x4)�̉��̑g�ݍ��킹�����݂��邩��ł��B �����ŁA��̎��g���P�ɑ��A2�{�̉������S8�x�A3/2�{�̉������S5�x�A4/3�{�̉������S4�x�i7�́j�ƌĂ�ł���A ���������ɑ����悭���a���鉹�ł��邱�Ƃ��s�^�S���X�����������̂ł��B �@���̎���ɃI�N�^�[�u�A���S5�x�A�]�X�Ƃ������t���g���Ă�����������܂��A ���R���ۂƂ��āA���g����2�{�ɂȂ�Ɠ��������P�I�N�^�[�u�����Ȃ����悤�ɒ������܂��B����͉��̂ł��傤�B �@(��) �Ȃ��u�I�N�^�[�u�v�Ƃ����P�ʂ����邩�H �@11�͂̋��U�E���ł��o�Ă��܂����A�悸�͉��̐}�����Ă��������B �P�{�̌���(1)�A���̌����͂����ĐU��������ƁA���̔g�͗��[�Ɍ������Đi��(a)���A ���̗��[���Œ肳��Ă���̂ŁA�[�ɓ��B�����g�͔��˂��ċt�����ɐi�݂܂�(b)�B 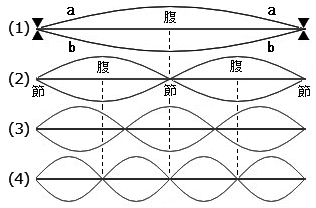 ���̌��ʁA�[�Ɍ������Đi�ޔg�ƁA���˂��Ė߂��Ă����g���d�Ȃ��āA
���ɂ͐}�̂悤�Ȋ�{���g��(1)�Ƃ��̐����{(2)(3)(4)�̒��g�������܂��B
���̒��g���A�����ŗL�U���̐����ł��B
���̌��ʁA�[�Ɍ������Đi�ޔg�ƁA���˂��Ė߂��Ă����g���d�Ȃ��āA
���ɂ͐}�̂悤�Ȋ�{���g��(1)�Ƃ��̐����{(2)(3)(4)�̒��g�������܂��B
���̒��g���A�����ŗL�U���̐����ł��B�@�����ł͐����̓s����A�g�̐U���͓����傫���ŕ`���Ă��邪�A ���ۂɂ́A�U�����ɔ���Ⴕ�ĐU���͏������Ȃ�̂ŁA�U�����������Ȃ�ƐU���͎���Ɍ���(��)���܂��B �@���ɁA���ɐU����^�����Ƃ��ɔ�������g�̋��U�E���̊W���l���Ă݂܂��B �}���c�����Ɍ���ƁA���̊�{�g�̕�(�U�����ő�)�̂Ƃ����2�{�g(2)��4�{�g(4)���߂ɂȂ�A3�{�g�͕��ɂȂ��Ă���B ����́A2�{�A4�{�g����{�g�ɋ��U���₷����Ԃɂ��邱�Ƃ������Ă��܂��B ���l�ɁA2�{�g�̕��̂Ƃ����4�{�g���߂ɂȂ�A3�{�g�͔��[�Ȉʒu�ɋ��܂��B �������|�C���g�ŁA��{�g��2�{�g�݂͌��ɋ��U�A2�{�g��4�{�g�݂͌��ɋ��U���܂��B ���̊W����ʘ_�Ō����ƁA�Q��n��{�̔g�in=0,1,2,3,����j�݂͌��Ɏ��R�ȋ��U�W�ɂ���܂��B���̊W���I�N�^�[�u�̒P�ʂł��B (��) ��L�ŐU�����������Ȃ�ƐU���͎���Ɍ�������ƌ������͎̂��R���̂��Ƃł��B ���ꂪ�����ŁA����{�������̎��g���Ƌ�����ƁA���̔{���͋t�ɋ����Ȃ邱�Ƃ�����܂��B  �@������̎����I�ȉE�}�̗�́A���̕Е��������Ɍq���A�����Е��Ɋ��Ԃ��o�R���Đ���t������ł��B
������@���ĐU��������ƁA���̐U�������ɓ`����Č����㉺�ɐU�����A���̐L�с^����݂Ŋ��Ԃ����E�ɉ�]���A�����㉺�ɉ^������Ƃ����d�g�݂ł��B
���̐U���ߒ��͏�L�Ɠ����ł��B���Ƃ͑z�����Ă݂Ă��������B
�@������̎����I�ȉE�}�̗�́A���̕Е��������Ɍq���A�����Е��Ɋ��Ԃ��o�R���Đ���t������ł��B
������@���ĐU��������ƁA���̐U�������ɓ`����Č����㉺�ɐU�����A���̐L�с^����݂Ŋ��Ԃ����E�ɉ�]���A�����㉺�ɉ^������Ƃ����d�g�݂ł��B
���̐U���ߒ��͏�L�Ɠ����ł��B���Ƃ͑z�����Ă݂Ă��������B�@���̐U���̘b�́A���̎��g���ɒu�������Ă��������Ƃł��B ���܁A��{�g�̎��g���i��j���u�h�v�ɂ����Ƃ��A����2�{�����u�h�v�Ɠ����悤�ɒ�������̂́A���̂��B �����̉������Ă���Ɗ�����̂́A��}��(1)��(2)�A(2)��(4)�̔g�`�����U�W�ɂ����āA�����݂��ɍł��悭���a���Ă��邩��A���o�����o����̂��Ǝv���܂��B ���̂��Ƃ́A12�͂ň�����������������ł��܂��B �����Ƃ͂Q�̉��������ɖ�Ƃ��A�������g������Ⴂ���g�������������g���̉��̂��Ƃł�����A���Ƃ��A��{�g��2�{�g�̊Ԃł͊�{�g�Ɠ������g���̍���(�Q�{���|�P�{�����P�{��)����������̂ŁA��{�g��2�{�g�͓����ƍ��o����̂��낤�Ǝv���܂��B ���ǂ̂Ƃ���A2�{�A4�{�A8�{�A�̂悤�ɁA�Q��n��̉����ƂɁA��́u�h�v�Ɠ����悤�ɒ������鉹�ɏo��̂ŁA ���̊Ԋu���u�I�N�^�[�u�v�Ƃ����P�ʂŕ\�킵���̂��낤�ƍl���܂��B ���o���A���������g����ŔF���������Ƃ�˂��~�߂��s�^�S���X�́A���́u�I�N�^�[�u�v�Ƃ����P�ʓ��ŁA�݂��ɒ��a���鉹��ςݏグ��12���K�����グ�܂����B �ł́A�ǂ̂悤�ɂ���12���K��������������͂Ő������܂��B  �@�@ �@�@
  �T�D�s�^�S���X�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@�~-�t�@�A�V-�h�Ԃ������Ȃ̂́H
�T�D�s�^�S���X�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@�~-�t�@�A�V-�h�Ԃ������Ȃ̂́H �U�D���ω����Ə��������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@���ꂼ��̕��݂Ɠ���
�U�D���ω����Ə��������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �E�E�E�@���ꂼ��̕��݂Ɠ��� �V�D�e�����̓����A�����̘b�^���̒��a�Ƃ�
�V�D�e�����̓����A�����̘b�^���̒��a�Ƃ� �W�D���a���E�s���a���ɂ���
�W�D���a���E�s���a���ɂ����@  �X�D���R�ɔ������鉹�͂��ׂĐ����g�̑g�ݍ��킹�@�@�@�@�@�@�@ �E�E�E�@�{���̒a��
�X�D���R�ɔ������鉹�͂��ׂĐ����g�̑g�ݍ��킹�@�@�@�@�@�@�@ �E�E�E�@�{���̒a�� 10�D�n�[���j�b�N�i�����g�E�{���E���a�j�� �{����
10�D�n�[���j�b�N�i�����g�E�{���E���a�j�� �{���� 11�D������������߁A�{�������F�����߂�
11�D������������߁A�{�������F�����߂� 12�D�a���E�����E���Ȃ艹�E�n�[���j�[�@�@�@�@�@ �E�E�E�@�����̓�F�Y��ȉ��ƌ��ȉ�
12�D�a���E�����E���Ȃ艹�E�n�[���j�[�@�@�@�@�@ �E�E�E�@�����̓�F�Y��ȉ��ƌ��ȉ� 13�D���U�E���E�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E�@�Q�y���̔@��
13�D���U�E���E�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E�@�Q�y���̔@�� 14�D���̐��藧���F�e�g���E�R�[�h�iTetraChord�j�@�@�@�@�@�@�E�E�E�@�Z���K�̓�
14�D���̐��藧���F�e�g���E�R�[�h�iTetraChord�j�@�@�@�@�@�@�E�E�E�@�Z���K�̓� 15�D�ܓx���}�E�����ƗՎ��L��
15�D�ܓx���}�E�����ƗՎ��L�� |