 (卓上の音楽) |
音楽の原点を探る |
画像加工広場 老夫婦の旅記録 |
１．背 景普段の会話で当たり前のように飛び交う言葉の中にも解らないことが沢山ある。音階ができた背景は？、美しい音色とは？、音色を決める倍音の正体は？、ハーモニーの正体は？、 楽しい／悲しい響きとは？、楽曲の仕組みは？、等々、関心ごとは沢山あり、これらを自然現象の中から学ぼうとした。 人は、本能のままに音楽との繋がりを築いてきた。ならば音楽は人為的に考えられた約束事ではなく、自然現象の中から生まれた事象だろうと推察できる。 たとえば、５度の調和、倍音列の響き、差音のハーモニー、規則的リズムの中の不規則な揺らぎ、など、音楽の原点が自然法則の中にある。 その自然法則というのは実に合理的に出来ており、足し算より引き算の美意識の方が合理性に叶う。 そう考えると、音楽ありきで総花的に学ぶより、身近な自然現象の中から音楽を学んだ方が、理解が深まることを実感した。 そこで、これまで断片的に得た音楽の知識を、復習と整理を兼ねて備忘録のつもりで纏めてみました。
２．自然現象の中から音楽を学ぶと理解しやすい ・・・ 音楽と人の本能
３．和む音には、不規則な揺らぎがある ・・・ Simple is Best
４．鍛冶屋の鉄打つ音から音楽の存在を予想 ・・・ ピタゴラス音律の誕生
５．ピタゴラス音律 ・・・ ミ-ファ、シ-ド間が半音なのは？
６．平均音律と純正音律 ・・・ それぞれの歩みと特徴
７．各音律の特徴、音程の話／音の調和とは
８．協和音・不協和音について
９．自然に発生する音はすべて正弦波の組み合わせ ・・・ 倍音の誕生
10．ハーモニック（高調波・倍音・調和）と 倍音列
11．基音が音程を決め、倍音が音色を決める
12．和音・差音・うなり音・ハーモニー8章で協和音・不協和音について説明していますが、そもそも音が調和するとはどういうことか、自然現象から見ていきます。 9章でも合成音について部分的に触れていますが、もう少し詳しく説明します。 複数の音から和音（chord）を作ったとき、互いの音の重なり具合によって、 音の調和、あるいはハーモニー(harmony)という言葉を使います。 「ハモる」とは、互いの音がよく溶け合ったときに使う言葉です。 ここで音がうまく重ならない（調和しない）と、不協和音になるが、不協和音だからといって嫌な音とは限らない。 ときには緊張感のある心地よい響きを与える音にもなり得ます。 ハーモニーは、通常、メインのメロディと違う音程のメロディーを重ねるように演奏することであり、 基本的にはメロディー(主旋律)に対して３度下、または３度上の音程で演奏することだそうです。 9章で音の足し算・引き算の話が出ましたが、ここでは具体例を使って話を進めます。 和音は複数の音の振幅を足し算した合成波であり、差音は２つの音の周波数の差によって生じる新しい音波のことです。 ■ 差音の謎 最初に「差音を聴いて音程を合わせる」という話を聞いたとき、その意味が理解できなかった。 差音がどうして発生するのか、鳴らしてもいない音がどこから聴こえるのか、など。 振り返れば、10章の倍音でも同じような現象があったのに、そこでは素直に理解できた。差音はどうか。 倍音は、１つの音を鳴らしたとき、それより高い周波数に複数音が発生し、音色に寄与します。 差音は、２つの音を鳴らしたとき低い周波数に差音が発生し、音域を広げたハーモニーに寄与します。（複数の音源があれば複数の差音が発生します。） ■差音は実際に聴きとれるか 差音の周波数が低いときは、その差音で変調された基音を「うなり」音として聴いているので解りやすいが、 差音の周波数が高くなって音波として聴いたとき、はたして差音を実際に聴き取れるか。 純粋な正弦波による差音を試し聴きしてみれば、何となく解ったつもりですが、 実際に、たとえばバイオリンのように倍音を多く含む楽器音でどうかといえば、差音を独立音として聴き取りは難しいです。 鳴るはずの差音が、いろんな周波数の倍音から発生する差音と複雑に入り込んで、１束になった重音として聴いてしまうからです。 このような差音は、ハーモニーに影響を与えることを次の例で見ていきます。 ■ 和音と差音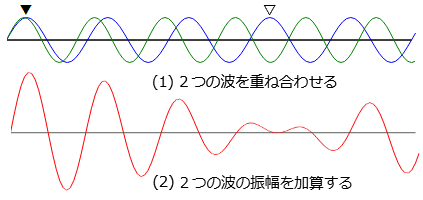 
右図の例では、(1)２つの音波を重ね合わせたとき、▼点で位相が重なり、▽点で位相が逆転している。
(2)この2つの音波の振幅（音量）を横軸に小刻みに加算していくと、重なった▼点で振幅は最大になり、位相が逆転した▽点で振幅は打ち消されゼロに近づく。
このように、２つの波の振幅を足し算したのが、和音であり、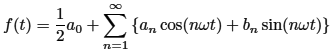
右図(2)で示す２つの音の合成波です。この波形(2)は、9章で説明したフーリエ級数という式で表わすことができ、音の解析には欠かせない数式です。 ２つの音が完全に重なれば周波数比1:1の一つの音になり、重なり▼点が無限になるので、音量だけは２倍になるが、ハーモニー効果には繋がらない。 合成波形(2)の場合は、音の重なり具合が少なく、振幅の頂点を結んだ包絡線を見ると、ゆるやかに波を打っており、これが「うなり」音になるのです。 この２つの波の重なり具合、つまり、差音によって、協和音・不協和音・うなり音の何れかが新たに発生します。 では、「うなり」音はどういうときに発生するか。 聴覚特性は、人によって異なるが、およそ20Hz～20KHzの音が聞こえます。 と言うことは、この差音が、およそ20Hz以下の音は人の耳では聞こえないので、この差音が「うなり」音として聞こえるのです。 この差音が20Hzより高い音は単独の音波として聞こえるので、これが協和音・不協和音になるのです。 上図(2)の波形は、元の綺麗な波形に比べて、かなり乱れた波形になっています。 つまり、この２つの音がうまく調和しないから乱れた音になるのです。これらの事実を纏めると以下のようになります。 ・２つの音の重なり具合で、調和したり、乱れたり、うなり音になったりする。 ・この音の重なりは、２つの音の周波数の差（周波数の高い音－低い音）で決まり、これを差音と言う。 ・この差音が、うなり(beat)音／協和音／不協和音の何れかになる。 ・差音が、およそ20Hz以下になると、うなり音として聞こえる。（聴覚特性は、およそ20Hz～20KHz） ・言葉を変えれば、綺麗な音・嫌な音は、複数の音を合成した波形を見れば分かる。 具体的な例で云えば、たとえば、ラ音440Hzと１オクターブ上のラ音880Hzを同時に鳴らせば、その差音は440Hzであり、下のラ音と一致する回数だけ音の波が重なるから最もよく調和します。 この重なり回数が極端に少なくなり、たとえば、「ラ音」の440Hzと444Hzの音を出すと、その差4Hzだけ周波数が重なります。 この4Hzの音は人の耳では聞こえないが、440Hzの音を4Hzで振幅変調した音、つまり1秒間に4回のうなり(ビート)音として聞こえます。 これが複音ハーモニカでいうビブラート音です。 イ短調の複音ハーモニカ(Am)のラ音は、低音220Hz±2Hz～440Hz±4Hz～880Hz±8Hz～高音1760Hz±16Hz、のように音程によってビブラート音を変動（2Hz～16Hz）させています。 では、440Hzと490Hzの音を鳴らすとどうなるか。ここでは50Hzのうなりが生じるが、「うなり」回数が多くなると、「うなり」ピッチが細か過ぎて、人間の耳はそれを「うなり」としては知覚できなくなり、代わりに50Hzの「音波」として知覚してしまうのです。 これが音波としての差音の正体です また、ラ音440Hzと１オクターブ下のラ音220Hzを同時に鳴らすと、220Hz（=440Hz-220Hz）の差音が生じ、１オクターブ下のラ音(220Hz)が差音で増幅されたことになります。 鳴らしてもいない筈の音が聞こえるという、この差音が一体どこで鳴っているのか、後で説明します。 もう一つの見方として、周波数比でみるとどうなるか。と言うのは、人の耳では音程の差は周波数比で認識されるからです。 そして、この音程の差こそ、差音になるからです。 たとえば、「ソ」と「ド」を同時に鳴らしたとき、２つの音の周波数比は「2:3」であるから、その周波数比の差は、ソ－ド＝(3/2)－(2/2)＝1/2、になる。 これが何を意味するか。 ２つの音を鳴らしたのに、「ソ・ド・１オクターブ下のド」の３つの音が鳴っており、この「１オクターブ下のド音」こそ差音であり、この差音が音域を広げる音として新たに発生した音になるのです。 当然のことながら、この３音はよく調和します。 すなわち、周波数の差だけ重なり（上の図(1)の▼点）が生じ、その重なりが多いほど、重なる周期が基準の音と調和して規則正しい波形になるということです。 調和した音の規則的な合成波形は、下に示す波形図からその様子が分かるでしょう。 差音の発生で、よく知られている例があります。 基本となる音「ド」の周波数を１とすれば、「ミ」の周波数比は5/4、「ソ」の周波数比は3/2、したがって「ミ」と「ソ」の和音を鳴らすと、２オクターブ下の「ド」音が聞こえてきます。 すなわち、ハーモニーは周波数の引き算によって発生するので、ソ(3/2)－ミ(5/4)＝ド(1/4)になる。（１oct.上は1*2、２oct.上は2*2、１oct.下は1/2、２oct.下は1/4） この「ド・ミ・ソ」はよく調和する音で、主要三和音（Ⅰ、Ⅳ、Ⅴ）の一つ、「トニック」コードです。 [ うなり音と調和する音の図解： ] くどいようですが、右下図の最初の例は「うなり」の例です。 220Hzと222Hzの音が重なると2Hzの差音が発生するが、人の耳では2Hzの音は知覚できず、この220Hzと222Hzの音波が毎秒２回だけ重なることによって「うなり」音として聞こえる。 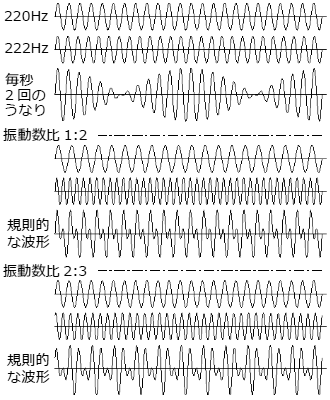 440Hzと444Hzの音を同時に鳴らしても同様、4Hzの差音が発生し、毎秒４回の「うなり」音が聞こえる。 では、440Hzと500Hzの音を同時に鳴らすとどうか。 その差音60Hzが生じるが、これは人の耳で知覚できる音なので「うなり」音ではなく、60Hzの音波として聞こえる。 つまり、440Hzと500Hzと60Hzの３音が聞こえるのです。差音も一つの音波です。 右図に戻って中段に、周波数比1:2の夫々の波形と2つの合成波を示し、更に周波数比2:3の波形と2つの合成波を示しています。 これまでに何度も出てきたが、周波数比1:2、2:3は共によく調和するので、夫々の合成波も規則正しく綺麗な波形であることが図から解ります。 ■ うなり音、協和音のサンプル 上で述べた事柄を実際の音で確かめてみます。 ①220Hzと222Hzの音が重なった差音2Hzのうなり音。 ②440Hzと444Hzの音が重なった差音4Hzのうなり音。 ③440Hzと500Hzの音が重なった差音60Hzの音波。④400Hzと500Hzの音が重なった差音100Hzの音波。 ⑤ド音と完全５度離れたソ音と、その差音（１オクターブ下のド音）の３音。 ⑥ド＃とソ音と、その差音（１オクターブ下のラ～ラ＃）の３音。 これらを再生したサンプルを下に示します。 差音を含めてそれぞれ３音がどのように聞こえるか確かめてください。（何れもサイン波で音を生成しています） 実際の音の例 ： Ａ｜①と②の音の比較｜ Ｂ｜③と④の音の比較｜ Ｃ｜⑤と⑥の音の比較｜ ■ 鳴らしてもいない差音が、どこで鳴るのか 10章で倍音について説明しました。たとえば「ド」音を鳴らしただけなのに、「ソ」や「ミ」の音も同時に発生(10章の倍音列)することがあります。 これらの倍音は共鳴の仕方によって大きさに差はあるが、音色を決める重要な要素です。差音についても同様の現象があります。 ２つの音の差が人の耳に聞こえない周波数だと、その差の数だけ波形が重なって振幅が大きくなるため、それが「うなり」音として聞こえます。 その差音が2Hz、4Hzの場合の「うなり」音が聞こえることを確認してください。 一方で、その「うなり」の周波数が高くなったとき、どのように聞こえるか。 その差音が60Hzと100Hzの場合の「うなり」音を聞いてみると、 そのうなり回数が多すぎて「うなり」音には聞こえず、１つの「音波」として知覚して聞こえてきます。 「うなり」音から単独の音波に変わっていく境界は人によって異なるが、およそ20Hz辺りになります。 この２つの同じレベルの音を聞いたとき、本来無い筈の音が聞こえるという現象をバロック音楽時代の作曲家タルティーニ等によって発見されたそうです。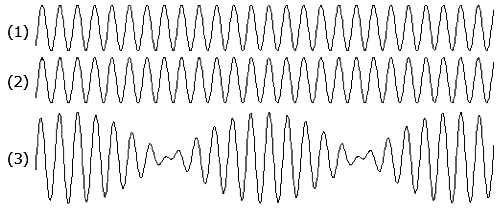 
■合成波の包絡線が差音右図は、差音を理解するための例です。 (1)は660Hzの音波を、 y = sin(660x) を仮定して描いた波形、 (2)は600Hzの音波を、 y = sin(600x) を仮定して描いた波形です。 (3)は２つの音波を重ね合わせの原理で足し算、y = sin(660x) + sin(600x) を描いた和音の波形です。 この(3)の合成波形の振幅の頂点を結んだ包絡線を描くとそれが「うなり」音の波形になります。 つまり、(1)の波形と(2)の波形の振幅を足し算した和音の波形(3)の包絡線の波形が差音であり、この例の包絡線は60Hzの差音の波形になります。 言い換えれば、上図(3)は１秒間に60回の「うなり」音を発生するということですが、１秒間にこんなに細かく「うなり」音が発生しても、人の耳には「うなり」としては識別できず、１つの音波と知覚してしまうのです。 したがって、660Hzと600Hzの音が同時に鳴ったとすれば、ここに60Hzという差音が新たな音波として発生したことになります。 上図(3)の２音の合成音を試聴すると、差音の様子が把握できます。 ◆もう一つ、２つの音440Hzと440Hz＋nを同時に鳴らし、ｎを徐々に上げて（n=1,2,4,8,･･･,100）いったときの差音の変化の様子も視聴してください。 「うなり」音が次第に重音に変わっていきます。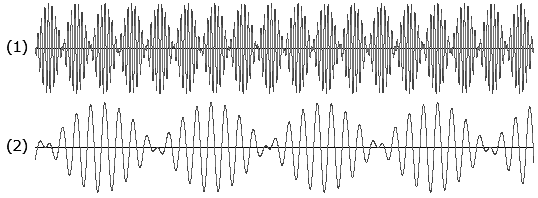 
因みに、n=100の最後の音500Hzと440Hzを同時に鳴らしたときの合成波の中に現れる60Hzの「うなり」は人の耳には音波として聞こえるが、これを時間軸で拡大して見ると上図(1)、(2)の波形になります。(1)は0.3秒に拡大した波形、(2)は0.258秒に拡大した波形です。 何れも波の頂点を結んでできた包絡線の波が60Hzの音波として鳴っていることになります。 周波数の高い音波も、時間軸で拡大して見ると、ごく短い時間内では「うなり」音になっていることが分ります。 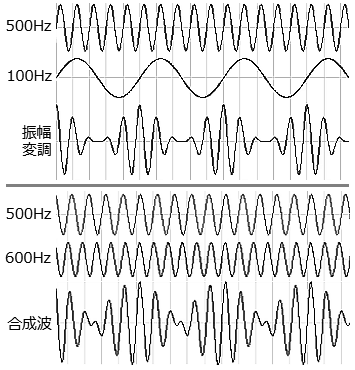 ■差音は振幅変調とよく似ている 振幅変調は、音声を遠くへ送るため、高い周波数の電波信号を音声信号で強弱に変化（振幅変調）させて伝送するときに使われます。 通常のＡＭ(Amplitude Modulation)放送局は、500KHz以上の搬送波を使用して、20Hz～20KHzの音声信号を送信しています。 右図上段は、500Hzの搬送波を100Hzの音波で振幅変調したときの波形、下段は500Hzと600Hzの波を合成したときできる差音100Hzの波形です。 両者はよく似ていますが、振幅変調より合成波の方が周波数が僅かに高く、500Hzと600Hzの合成波の場合は高い方の600Hzの搬送波を差音100Hzで振幅変調したような波形になっていることが分ります。 つまり、２つの音を同時に鳴らしたとき、高い方の音を差音で振幅変調した波形とほぼ同じになるということです。 ■ 聴覚の錯覚現象（錯視と錯聴） 視覚の認知現象にマッハ効果という錯覚現象があり、これと同様に聴覚にも錯覚があります。 ・マッハ効果と言うのは、図のように濃度差のある境界部分で、明るい部分はより明るく、暗い部分はより暗く見える効果のことで微分効果の一つです。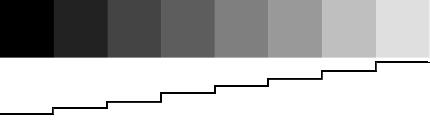 
この効果は、人が自然の中で生きるため、危険が迫った瞬間にそれを察知・防衛するため、何らかの変化点を迅速に察知する本能の結果であろうと考えられます。
これは、ドイツの物理学者 Machにより命名された。（音速をあらわすマッハと同じ人物。）
一方、常に平和で居たい本能も働くので、これは積分効果といって、複雑で激しい変化を平均化して、何事も穏やかに見ようとする本能です。聴覚でも同様の錯覚があり、平坦な音の流れの中に突然音が変わると、それをより鮮明にしようとする本能が働いてその差を多く感じるでしょう。 
逆に、複雑に変化するメロディ音の中に間違った音が入り込んでも気付かないで見過ごしてしまうでしょう。・もう一つ、右の絵は実際には同じ大きさだが、小さい円に囲まれると大きく見え、大きい円に囲まれると小さく見えます。 ・同様のことが聴覚でも起こり、下の五線譜で同じ休符でも１小節目の休符より２小節目の休符のほうが短く感じてしまう時間縮少錯覚というリズムの錯覚が起きます。  （１）きれいに響く音とは 何度も出てくる言葉ですが、きれいに響く音か否かは合成波形を見れば直ぐ分かる。 前述例のように、周波数比が(1:2)、(2:3)などの音が重なれば周波数の差だけの差音が発生し、 その合成波形をみると周波数比が(1:2)、(2:3)の何れのも規則正しい波形になっていることが分かります。 ２つの音がよく調和するから規則正しい合成波形になるのです。 そして、２音の整数比が単純なものほど、合成波は規則正しい波形で、綺麗に調和するということです。 調和しない汚い音は、たとえば、1:2の周波数比が1:1.9などの複雑な比率になったときであり、 重なった波形も複雑に乱れています。（下記(2)の図、発泡スチロールを擦る音の波形のように） ■ 差音が単純な整数倍のとき、よく調和する 最も調和する重音は完全一度(同音)で、波形が完全に重なって音量は増えるが差音は発生しないため、ハーモニーは得られません。 完全8度(オクターブ)の差音は下の音と一致。 つまり、(2倍のド)－(基音のド)＝(基音のド音）が発生するから完全に一致する重音だが、差音が基音と重なるため２音しか聞こえず音域の広がりは感じません。 何度も出てきましたが、完全4度・5度の差音は非常に調和しやすい重音になります。 たとえば、完全5度(周波数比2:3)の例では、「ド」と「ソ」を同時に鳴らすと、１オクターブ下の「ド」の音が聞こえる。 これは、基音のドの周波数を１としたとき、ソード＝(3/2)－(1)＝(1/2)、つまり１オクターブ下のド音が差音として新たに発生するため、 ３音がバランスよく聞こえ、音域の広がりを感じるのです。（完全4度の場合も同様です） ■ 長短3度の音程差も調和する たとえば、長3度の「ド」と「ミ」を同時に鳴らすと2オクターブ下のド音が聞こえてくる。理由は、ミ(5/4)-ド(1)=(1/4)、つまり、２オクターブ下のド音が発生している。 短3度の「ミ・ソ」間では、ソ－ミ＝ソ(3/2)－ミ(5/4)=(6-5)/4=1/4、つまり、２オクターブ下のド音が発生している。 短3度のレ・ファ間では、(4/3)-(9/8)=(32-27)/24=5/24=(5/3)X(1/8)では、3オクターブ下のラ音が発生する。等々。 いずれの場合も、差音が基音のオクターブ違いとか、主要３和音に該当する音になっている、などの理由で調和すると言えます。 （上記の周波数比の意味は、「6章の純正音律音程表」で分かります。）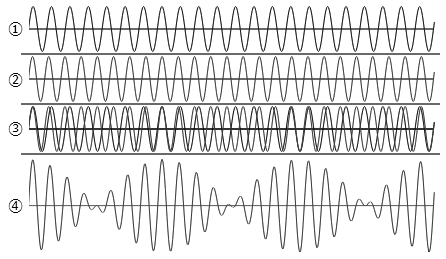 
■ 差音が綺麗なハーモニーを作る
もう一つ分かりやすい例を挙げると、右図は①440Hz(ラ：A4)と②550Hz(ド#、C5#に相当)を同時に鳴らしたとき、
その重ね合わせた音は③になり、①と②の振幅を加算すると合成波④になる。
③は２つの音の重なり具合を示すもので、重なりが多くなるに従って④の振幅が大きくなっており、
位相が反転するに従い、振幅が小さくなっていることが解ります。この④の合成波形こそ和音です。 そして、この波形が規則正しい綺麗な波形であればよく調和した音、不規則に乱れた波形であれば不協和音になります。 合成波④の振幅の頂点を結んだ包絡線が「うなり」であり、その回数は、550Hz － 440Hz = 110Hz(ラ：A2)、つまり、1秒間に110回の差音が発生することになる。 したがって、④の合成音には、440Hz、550Hz、差音110Hzの３つの音が含まれており、 ここで新たに発生した110Hzの差音の存在が、きれいなハーモニーを得るうえで大切になるのです。 ③の２つの音の重なり具合からも「うなり」の様子が見えます。この「うなり」回数が増えれば調和音になります。 因みに、この差音110Hz(ラ：A2)の音は、440Hz(ラ：A4)の2オクターブ下の音であるから、440Hzと550Hzの音はよく調和する音と云うことになります。 つまり、110Hz音の4倍音が440Hz音、5倍音が550Hz音、何れも整数倍音になっています。 では、440Hz音と550Hz音を重ねた音、新たに発生した差音110Hzはどのように響くでしょうか。 ▼｜２つの合成音と差音効果を視聴する｜▼ （２）嫌な音とは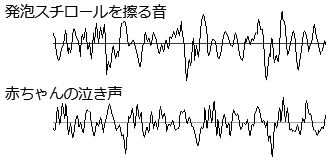 
7章で述べた音符上の不協和音が響きの悪い嫌な音かと云えば、そうではない。
メロディによっては、ときに美しい響き、心地よい印象を与える音にもなり得ます。ここで言う嫌な音とは、あの音だけはどうしても耐えられないという、人に共通する耐えがたい音のことで、 ガラスを引っ掻く音、発泡スチロールを擦る音、歯を治療するときの音、赤ちゃんの泣き声、など。 右図からも分かるように、先ほど見た規則的な波形とは異なり、かなり不規則で乱れた波形になっています。 嫌な音の共通点は、音の周波数が普段聞き馴れない非常に高い音で2000～4000Hzということです。 人間の耳が最も反応しやすく不快に感じる音の周波数も2000～4000Hzで、防犯アラームもこの周波数に合わせて作られているそうです。 逆に、人の耳では知覚できない低周波は5～9Hzでも、これがエネルギーを持ったときは、その振動が体に伝わって内臓を揺らし不快になるようです。 ▼| 嫌な音を試聴する |▼ 上図のように、ここで赤ちゃんの声を取り上げたのは、実にうまく出来ているからです。 赤ちゃんの声は可愛らしく、普段は400～600Hzの間というが、何かを訴えて大声で泣く時だけは、1700Hz以上という高い音です。 これは、お母さんや周囲の人に、助けを求める悲痛な声を伝えるため、赤ちゃんが生きるための本能として、この高い声を出すものと考えます。 しかし、人がこれだけ高い周波数で声帯を振動させているとは考えにくいので、おそらくは本能的に高周波の倍音を大量に出しているのだろうと想像します。 
13．共振・共鳴・同調 ・・・ 群軽折軸の如く
14．調の成り立ち：テトラ・コード（TetraChord） ・・・ 短音階の謎
15．五度圏図・調号と臨時記号 |
Copyright ©2019 - Smo. All rights reserved. Last Updated 09/18/2019.