 (卓上の音楽) |
音楽の原点を探る |
画像加工広場 老夫婦の旅記録 |
１．背 景普段の会話で当たり前のように飛び交う言葉の中にも解らないことが沢山ある。音階ができた背景は？、美しい音色とは？、音色を決める倍音の正体は？、ハーモニーの正体は？、 楽しい／悲しい響きとは？、楽曲の仕組みは？、等々、関心ごとは沢山あり、これらを自然現象の中から学ぼうとした。 人は、本能のままに音楽との繋がりを築いてきた。ならば音楽は人為的に考えられた約束事ではなく、自然現象の中から生まれた事象だろうと推察できる。 たとえば、５度の調和、倍音列の響き、差音のハーモニー、規則的リズムの中の不規則な揺らぎ、など、音楽の原点が自然法則の中にある。 その自然法則というのは実に合理的に出来ており、足し算より引き算の美意識の方が合理性に叶う。 そう考えると、音楽ありきで総花的に学ぶより、身近な自然現象の中から音楽を学んだ方が、理解が深まることを実感した。 そこで、これまで断片的に得た音楽の知識を、復習と整理を兼ねて備忘録のつもりで纏めてみました。
２．自然現象の中から音楽を学ぶと理解しやすい ・・・ 音楽と人の本能
３．和む音には、不規則な揺らぎがある ・・・ Simple is Best
４．鍛冶屋の鉄打つ音から音楽の存在を予想 ・・・ ピタゴラス音律の誕生
５．ピタゴラス音律 ・・・ ミ-ファ、シ-ド間が半音なのは？
６．平均音律と純正音律 ・・・ それぞれの歩みと特徴
７．各音律の特徴、音程の話／音の調和とは
８．協和音・不協和音について
９．自然に発生する音はすべて正弦波の組み合わせ電力会社から配電される商用電力は、殆ど歪みのない基本波（サイン波）に近い交流電圧(図1)です。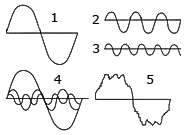 
それが、送電途中でいろんな障害波(図2･3)を受けて家庭に届いたときには、歪んだ波形(図5)のようになっています。空気中を伝播する電波も音波(音圧)も同じことで、常に何らかの障害物の影響を受けて波形に歪みが生じています。 その歪んだ波形(図5)は、正弦波の整数倍で合成された波(図4)であることを、 つまり自然界で発生する音はすべて正弦波(サイン波)の組み合わせで出来ていることをフランスの数学・物理学者のフーリエ男爵(1768〜1830年)が発見したのです。 ・・・倍音の誕生です。 後にフーリエ級数・フーリエ解析を生み出し、科学の進歩を飛躍させました。 その恩恵を受けて音楽も、特に楽器や音響設備などで大きな進歩を成し遂げました。 あらゆる分野で活躍するフーリエ解析は、ここ音楽演奏でも、音質・音色などを調べて評価するのに欠かせないものです。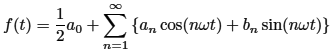 
ここでフーリエ級数を説明するつもりはないが、形だけ示すと次のようになります。周期的な波形f(t)は、すべてサイン波、コサイン波の綺麗な波形に分解できる(上図4)、と云うもので、上の式で表わされる。 おお雑把に言えば、時間軸ｔで振動するすべての波は、基音である角周波数 ω の波と、そのｎ倍音の波をすべて足し合わせることで表現できる、というものです。 たとえば、周波数ωのド音が発生して、それが伝わっていく間に、いろんな障害を受けて正弦波のｎ倍の波形に変化して伝わっていく、ということです。 空間を飛び交う電波も、地震波も、テレビ信号も、楽器の音も、人の声も、震動するものは全てこの式で表現でき、フーリエ解析という手段で波形を解析するのに欠かせない数学です。 上式のような、ある時間軸上の波形ｆ(t)を周波数領域ｆ(ω)へ変換することをフーリエ変換（FFT）と言っています。 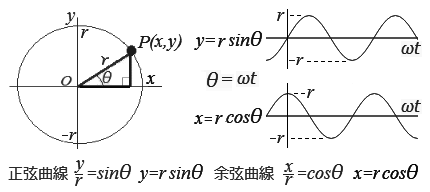 ■ 周波数解析： 正弦波の原理をもう少し説明します。 右の図で、物体Ｐが半径 r の円周上を反時計回りに回転するとき、 角度θだけ回転したときの円周上の点(x,y) の座標値は、y=r sinθ、x=r cosθ で表わせます。 これを見ると、点 x と y では位相が90度ずれていることが分かります。 円周上をぐるぐる回っているときの任意の点Ｐ（x,y）の値は上の式で表わしますが、 これを時間軸に引き伸ばしてみるとどうなるか。 円周を回転していた物体が、上図右側のように、ｙ軸に沿って上下運動し、それを時間軸に伸ばしてみた感じの波になります。 回転角θが時間の経過に沿って位相が変化することだから、1秒当たりに進む角度を角速度(角周波数)と言ってωで表します。 つまり、1秒でωだからｔ秒でθ=ωtになります。この結果、正弦波は、y=r sin(ωt)、x=r cos(ωt) で表わすことができます。 上で示したフーリエ級数は、上図の波形を合成した式と云うことになります。 冒頭の電力の話に戻って、自然に発生する波形(冒頭図5)に、どの周波数がどれ位の量含まれているかを調べるのが周波数解析です。 次に、実際の楽器音でその様子を見てみます。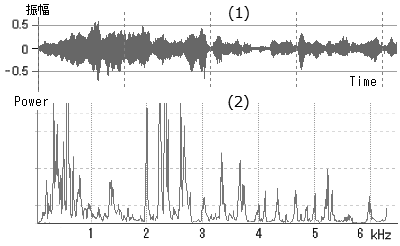 
右図(1)は演奏中の楽器音の波形の一部で、時間の経過に沿って音の振幅（音量）の変化を測定したものです。 図は横軸を秒単位で表示しているが、これを1000倍のミリ秒に引き伸ばしてみると、下図(1')のように振幅の違う正弦波の連続であることが分かります。 これに対して図(2)は、(1)の波形を、音の周波数とその振幅量に変換した図です。 このように、音の波形を周波数領域へ変換するのが上記のフーリエ変換です。 こうして図(2)を求めれば、どの周波数の音がどれ位の量出ているか解ります。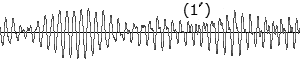 
周波数が分かれば音階のどの音が多く鳴っているかが解るのです。
この図自身はかなり縮小しているので細部は分らないが、この図では220Hzのラ音にピーク値があり、
次に247Hzのシ音、523Hzのド音、などの周波数が多く出ています。
2KHz以上にも多くのピーク値が見られるが、これ等は基音が鳴ることによって生じる、多くの倍音が出ているのです。同じ音を鳴らしているのに音色が異なることはよく経験します。音色は倍音の出し方によって影響を受けるので、周波数解析すれば倍音の出方が一目で解ります。 このことは、10章の倍音の項で事例をあげて詳しく説明します。 （この解析は、3章の「1/f ゆらぎ」の観測にも利用されます。） このような周波数解析は電波や音波だけでなく、多くの分野で画像解析にも利用されています。
■ 周波数解析で解ったこと： このように、上記の式を使って、音楽で扱う音を解析すると、次のようなことが解ってきました。 弦楽器や管楽器は比較的澄んだ音、打楽器は比較的濁った音というが、これらの音の周波数を分析してみると、いろんな周波数が含まれていることが分かります。 たとえば、「ド」を単音で出した場合でも、その中にはソ音やミ音、その他いろんな音が混ざって伝播していきます。（10章の倍音列を参照） 弦楽器や管楽器の音は、それを構成しているいくつかの周波数が簡単な整数比になっています。 特に、多くの音は、基本となる周波数と、その倍数の周波数になっていることから、 一般的な呼び名では、これ等を基本波と高調波と言っています。よく使うハーモニックという言葉は高調波のことです。 音楽では、これを基音と倍音と呼んでいます。 11章で詳しく出てきますが、この基音と倍音の混ざり具合（合成波）で音色が決まるということですから、 楽器ごとに基音と倍音の出し方に夫々工夫があります。 たとえば、バイオリンやオーボエは倍音が多く含まれ、ピアノは基音の響きに倍音をのせて鮮やかに響かせるため、調律が大切な楽器だそうです。 人の声は、意外にも基音と倍音が完全な整数比になっていると云われます。その理由は以下の通り、↓↓↓ ■ 人の声の伝わり方： 人の声でも多くのことが解りました。気管から出てくる空気をエネルギーとして声帯を震わせ、その震動が声道（平均で成人男性で17cm、成人女性で14cm程度）を通って声になって出てくる。 つまり、声帯の振動が基音となり、声道で共鳴させることによって、エネルギー分布の異なる音にして外へ出しています。 乱暴な言い方をすれば、人は声帯を震わせて、トランペットは唇を震わせて基音を作り、後は夫々の構造上の事情で倍音を生み出している。 それ故、大雑把に言えば、人の声はトランペットのような楽器とほぼ同じ原理で音声を作っているので、基音と倍音が完全な整数比になっていると言えます。(11章に関連事項) 赤ちゃんの可愛い声は、普段は400〜600Hzですが、何かを訴えて大声で泣く時だけは、1700Hz以上という高周波の音で、 この音域は人の声帯振動音では出せない高い音域ですが、これが出ているということは、基音(400〜600Hz)の他に倍音を大量に出していると想像できます。 これは、お母さんや周囲に、助けを求める声を伝わりやすくするため、赤ちゃんが生きる本能として、この高い音域を出しているものと考えられます。 人の声で倍音の出し方については、11章で少し付け加えてお話します。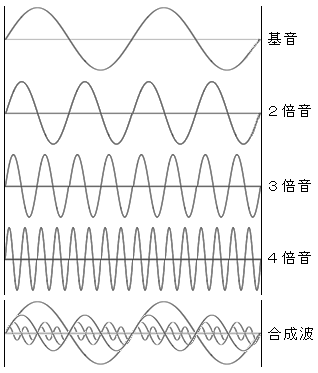 
■ 合成音の、振幅は足し算、周波数は引き算： 冒頭の例と重複しますが、フーリエの発見がどういうものか、話を前に戻して右図で整理してみると次のようになります。 １つの音(基音)を鳴らすと、伝播中にいろんな歪みを受け、その結果として複雑な波形になるが、 その複雑な波形も分解してみると、右図の２倍、３倍、４倍音、・・・の波形が重なって出来たものであり、その合成波の音になります。 実際の合成音のエネルギー(振幅)は、波の足し算になるので右図下段とは異なり、 各振幅を足し算した複雑な波形になるが、分解すれば右図の合成音のような波形の重なりになります。 右図は、説明のための図であり、実際の音には２倍、３倍、４倍音、・・・がこの大きさの波形で重なるものではありません。 次に、合成音の周波数はどうなるか： ２つの音が同時に鳴るとき、合成音の周波数には、足し算は無く、引き算だけ成り立ちます。 結局、合成音の周波数は基の２つの音と、その差音を含めた３つの音が聞こえることになります。 この様子を、足し算・引き算の形を例題で説明します。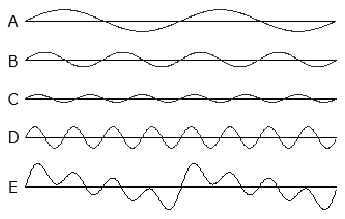 
■ 音の足し算・引き算の例：上記の例と少し形を変えて、実際の波の合成として見てみます。 複数の波の振幅を足し算した合成波の例： 右図でＡ、Ｂ、Ｃ、Ｄはそれぞれ周波数比が、 1:2:3:4の波形です。これ等を前式のフーリエ級数で足し算すると、Ｅの合成波形ができます。 計算式を使わなくても、振幅の幅を小刻みに足し算しても同じ結果になります。このＥが合成波です。 逆に言えば、Ｅの音が発生したとき、その波はＡ、Ｂ、Ｃ、Ｄの正弦波に分解できるということです。 では、合成音Ｅの周波数はどうなるか。 周波数比が、1:2:3:4の音Ａ、Ｂ、Ｃ、Ｄの音が同時に鳴ったとき、それらを合成した音Ｅの周波数は理屈のうえでは次のようになります。 Ｅの周波数は、Ａ〜Ｄ各音の周波数と、各音の周波数の差、から成り立っています。 この周波数差は、高い周波数から低い周波数を引き算した値で、差音として新たに発生する音です。 その数は、上記例では、D-C=1、D-B=2、D-A=3、C-B=1、C-A=2、B-A=1、だけ存在します。 結局、Ａ〜Ｄの音が同時に鳴ったとき、Ｅの音の周波数には、Ａ〜Ｄの周波数と差音の数だけの周波数が含まれていることになります。 しかし、この例の場合は、Ａ〜Ｄの周波数比が1:2:3:4という最も単純な整数倍になっているので、差音はすべてＡ〜Ｄの何れかの音になるので、この例では新たな差音は聞こえません。 ところが、たとえば、Ａ、Ｃだけを同時に鳴らしたときはどうか、これまで鳴っていないＢの音が新たに発生します。 ここでＡをド音、Ｃをソ音だとすれば、ソ-ド=(3/2)-(2/2)=(1/2)、つまり、1オクターブ下の「ド」が一緒に鳴るのです。これがハーモニーを生み出す音になります。（12章で詳しく説明します。） 一般には、同時に発生する複数の音は、必ずしも整数倍になっているとは限りません。 つまり、新しく発生した差音が、他の音と共鳴して増幅したり、打ち消しあって微弱になったりするので、計算通りにはなりません。 したがって、合成した音Ｅがどんな形になるかは、周波数解析してみないと解りません。 上記の例は、話を簡単にするため正弦波にしていますが、 特定の周波数だけの単純な音だけ鳴らしても心に響く音にはなりません。 複数の周波数の音が適当に配分されてこそ「良い音」ということですから、 人の声も楽器の音も、前述の倍音の含み方で綺麗な音色か否かが決まると言えます。 同時に鳴る複数の音の周波数を引き算すると、差音という新しい音が発生する。 この新たに発生した差音は、うなり音・ハーモニーを生み出す音なので、改めて12章で説明します。 
10．ハーモニック（高調波・倍音・調和）と 倍音列
11．基音は音程を決め、倍音は音色を決める
12．和音・差音・うなり音・ハーモニー ・・・ 差音の謎：綺麗な音と嫌な音
13．共振・共鳴・同調 ・・・ 群軽折軸の如く
14．調の成り立ち：テトラ・コード（TetraChord） ・・・ 短音階の謎
15．五度圏図・調号と臨時記号 | ||||
Copyright ©2019 - Smo. All rights reserved. Last Updated 09/18/2019.