|
画像圧縮：その２
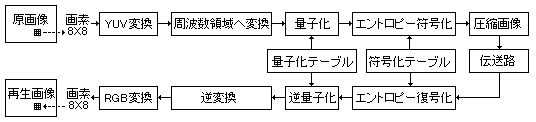
(1) ＲＧＢ色空間をＹＵＶ色空間へ変換（人の色識別能力特性への変換） (2) 画素のサンプリング（輝度と色情報は分けてサンプリング） (3) 空間周波数領域への変換（離散型コサイン変換を利用） (4) 各周波数成分を視覚特性に合わせて量子化（各周波数成分に視覚特性に合った歪みを与える） (5) 直流成分の線形予測（直流成分は周波数の中でエネルギー大きく、最も偏りが出やすい） (6) ハフマン符号によるエントロピー符号化（偏りをもった情報の符号化） であり、これらはすべて「画像圧縮：その１」で述べたことに対応しています。 （１）ＲＧＢ色空間をＹＵＶ色空間へ変換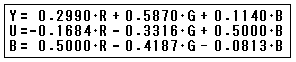 
ＲＧＢ色空間をＹＵＶ色空間への変換は右の式で表しますが、
ここでＹは輝度成分、ＵＶは色成分を指しています。このような表し方をするのは、人の視覚特性になるべく合わせるためです。 人の目はグレースケール（黒から白までの明るさの変化）に対する識別能力は高く、 色の識別能力はそれほど高くはありません。 このことは、ＲＧＢの３色を使う必要がないことを意味しています。 したがって、ＲＧＢをこのようにＹＵＶに変換しておけば、 人の目の能力に対する不要な情報が省きやすくなる訳です。 ★ 私たちが家庭で見るテレビでも同じようなことをしており、 ここではＹＩＱと云う座標軸に変換しています。 ★ これによって、まずは人の目の特性に合うように画像情報に偏りをもたせることができます。 （２）画素のサンプリング 人の目は、明るさの変化には敏感に、色の変化には鈍感に作用すると云う特性を利用して、 画像の色が変化する情報を間引くことで先ずはサイズ縮小しようとするものです。 ★ ＹＵＶと云う色空間へ変換したとき、上で述べたように輝度成分と色成分の重要度から個別にサンプリングします。 粗っぽくサンプリングすれば、画像の変化の激しい部分で情報が失われ、 平坦な部分では必要ない情報まで拾ってしまうことになります。 ＪＰＥＧでは、ＹＵＶに対して１：１：１、２：１：１、 ４：１：１の割合でサンプリングするという３通りがあります。 ４：１：１の割合でサンプリングするということは、 輝度情報Ｙを４画素拾う間に色情報ＵＶは１画素しか拾わないということで、 この場合は変化の激しい部分で色情報がそれだけ失われてしまいますが、 人の目から見て色情報は変化に対してそれほど敏感に応答していないので捨てても影響が少ないだろうと云えます。 したがって、一般には標準的な圧縮ではこの４：１：１の割合でサンプリングする方法が使われています。 ★ 先ほど、家庭のテレビではＹＩＱに変換していると云いましたが、 ここでも同じようなサンプリングを行っています。 つまり、人の目の感ずる輝度成分Ｙは、 面積の小さいところまで敏感に作用するので４ＭHzまで送り、 少し大きな面積になるとオレンジ色を見分けることができるので、この色を Ｉ信号として１．５ＭHzまで送り、 更に大きな面積になると、この Ｉ軸と補色になる緑とマゼンタ色まで見分けるので、 これをＱ信号として０．５ＭHzまで送っています。 これは、上記と同じくＹＩＱ信号を目の特性に合わせてサンプリングしていることになります。 （３）空間周波数領域への変換 何らかの変換を行なって画像に偏りを持たせることができれば冗長度を減らすことができると云ってきました。 空間周波数領域へ変換することは、信号をできるだけ特定軸上に集中させるようにするためです。 ★ 画像の一部を拡大してみると、それは画素の集まりであることが分かります。 各画素には色情報を持っており人はこの情報を光のエネルギー情報で感知しています。 と云うことは画素をエネルギーとして扱うこともできます。 周波数領域で各周波数成分の発生頻度をエネルギー量として見るのです。 ★ さて、画像を部分的（ＪＰＥＧでは８Ｘ８画素単位）に見ていくと、 ある部分では滑らかな状態であったり、また別の部分では変化の激しい状態であったりしています。 これらの変化の状態で一枚の画像を構成していることが分かります。 そこで、この部分的な画素の集まりの中で、画素値の変化の度合いを周波数の尺度で見ることができるのです。 ★ 画素の集まりである画像空間を周波数領域に変換する方法には沢山の種類があります。 アダマール変換、ハール変換、スラント変換、カルーネン・レーベ変換、フーリエ変換、・・・など他にも沢山ありますが、 処理が簡単で且つ周波数への変換誤差が少ない方法が一番よい方法と云えます。 その中で、ＪＰＥＧが離散型コサイン変換という方法を利用しているのは、 画像を周波数領域へ変換するときの部分領域が８Ｘ８程度だとその変換誤差が少なく、 演算アルゴリズムもそれほど複雑でなく、コスト面でも変換効率が優れているためです。 ★ 変換誤差だけを考えれば、周波数領域へ変換する画像の部分領域を大きくしていけば誤差は少なくなっていきますが、 その分、演算が膨大になり実用的でなくなります。 したがって、コンピュータで計算してもそれほど負担にならないサイズとして８Ｘ８程度が選ばれていると思います。 ★ ここで、各種変換方式の変換誤差がどの程度になるかは、論文に出ていることですが、 それを見ると、よく知られているフーリエ変換は変換誤差が一番少ないと云われながらも、 変換領域が無限に大きいときに成り立つ方式であって、その領域が８Ｘ８程度では誤差は大きなものになっています。 ★ 理想的には抽出した各周波数成分が、 他の成分と交絡することなく互いに独立した成分として抽出できれば一番よいことになりますが、 そのような変換方法は存在せず、 一般には一つの周波数成分に他の成分も一部が含まれてしますことになり、これが変換誤差になる訳です。 なぜなら、変換領域が８Ｘ８だと縦横共に８次以降の成分がカットされていまっているからです。 （高周波成分をカットすると折り返し歪みの影響が出てきますが、 これは別の機会にお話します。） ★ 領域が８Ｘ８程度のとき変換誤差が少なく最も優れた方法はカルーネン・レーベ変換と云われますが、 やはりコサイン変換に比べて処理に負担がかかり、まだコスト的に問題があります。  次のページへ
|
「画像圧縮：その１」の続きとして実際の圧縮方法を見ていきます。