（４）各周波数成分を視覚特性に合わせた量子化
次に、この空間周波数領域で各周波数成分をどう扱っていくかの話になります。
ここでもう一度、「画像処理の種類」のページで述べた人の目の特性を思い出してみると、 画像の変化の激しい複雑な部分は平均化するように、 また変化の少ない平坦な部分やそこから急に状態が変わるような部分は、 その変化点を注視するように見る習性があと云うことです。　 したがって、この特性をうまく利用しないとたいした画像圧縮にはならなくなってしまいます。
★　このような特性を考えると、先ずは直流成分（電気で云う直流と同じで変化のない、 つまり８Ｘ８領域の画素値の平均値）や一次、二次成分が大切で、 高次の成分はそれなりにカットしても（歪みを与えても）目にはそれほど大きな影響は与えないでしょう。 各周波数成分で不要と思われる成分をカットすることを量子化と呼んでもよいでしょう。　 たとえば、元が１００の値を持っており、その内４０が不要なら量子化値は６０と云うことになります。
★　実際にどのように量子化をしているかと云うことですが、 これは難しいことで、「圧縮したときの画質の満足度と圧縮率のトレードオフになる。」と曖昧なことしか云えませんが、 この後に出てくる各周波数成分の量子化テーブルは、 これが正しいと云う回答ではありませんが、 標準的に圧縮する場合の量子化値の目安になると思います。
しかし、この量子化テーブルでは直流成分を比較的多めにカットしているので、 三次元グラフィックス画像で見かけるような非常に滑らかな部分の多い画像では、 その部分に歪みの目立つ可能性があります。

（５）直流成分の線形予測
これは画像の中で近傍画素同士がよく似ている場合が多いと云うことで、 近傍の画素から注目画素値を予測してやり、その予測が正しければ注目画素の値は不要になります。
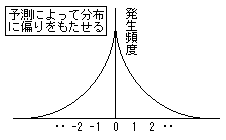
もちろん、予測が外れることも多いので、その予測値と実際値の差分値を分布で表してみると、 おそらくは図のようにゼロを中心にある拡がりをもった分布になるはずです。
すなわち、予測によって画像に偏りをもたせたことができれば、 以下のエントロピー符号化で発生頻度の多い差分値に短い符号を、発生頻度の少ない差分値に長い符号を与えることがことができる訳です。
★　このような予測方法の弱点は、現在の値によって次を予測する訳ですから、 伝送中にどこかでエラーが発生した場合に、そのエラーが次々と伝搬すると云うことです。
このため、永久に予測するのではなく一定領域毎に予測を初期化して、 そのエラー伝搬をくい止めるようにしています。

（６）ハフマン符号によるエントロピー符号化
どんな場合でもそうですが、情報に何らかの偏りがあるとその情報１個１個の発生頻度が変わってきます。
この発生頻度がまったくの一様である場合にはここで云うエントロピー符号化は価値がありません。　 ところが自然界では発生頻度がまったく一様に分布することは少なく何らかの偏りを持っています。
この事実をここで利用しようと云うことです。
★　これまでに何度も、「画像に何らかの偏りを持たせることができれば、云々」と云ってきましたが、 他の箇所で述べたと同様にその効果がここでも出てきます。
それは前にも述べた情報理論によって、最大情報量から平均情報量だけ情報量を減らすことができるからです。
これをエントロピー符号化と呼んでいますが、そのために何らかの効率的な符号語を定義しなければなりません。
★　上の図にあるように直流（ＤＣ）成分を線形予測したお陰で直流成分に偏りを出すことができました。　 したがって、発生頻度の一番高い、実際値と予測値の差分がゼロに一番短い符号語を与え、 次に発生頻度の高い差分値に二番目に短い符号語を与える、 と云う感じで符号語を定義していけば、冗長度の少ないかなり効率的な符号化ができます。
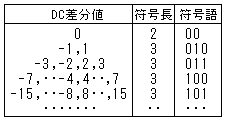
★　右の表は一部分だけを示していますが、直流成分の差分値に応じて与える符号語の例です。
これをハフマン符号と呼んでおり、ＪＰＥＧで実際に使われているものです。　 ここでは輝度情報の直流成分に対する符号例の一部しか示していませんが、 この他には、輝度情報の交流成分や、色情報の直流・交流成分それぞれにもっと複雑な符号が定義されています。　 しかし、考え方は同じことです。
★　以上、５つの工程を経てＪＰＥＧの画像圧縮が行われています。　 次に圧縮率や画質に最も影響する量子化について考えてみます。

具体的な量子化方法
ＪＰＥＧで画質が劣化するとか、圧縮率がどうかとか云う言葉を使いますが、 ＪＰＥＧの場合の画質の劣化度は殆どが量子化のところで決まります。
ここで示す図はほんの一例ですが、各周波数成分の量子化テーブルを示しています。　 縦横０から７までの各周波数成分に対して、 各数値は、画像空間を周波数領域に変換したときの各周波数成分の歪み量を示しており、 たとえば歪み量１６はその周波数成分を１６分の１にカットすることを意味しています。
ここで、周波数成分が８Ｘ８になっているのは、画像の部分領域８Ｘ８画素空間で周波数に変換しているからです。
★　また、上で述べたように、色情報は輝度情報より識別能力が低いので、 実際の量子化テーブルは輝度情報用と色情報用の２つを用い、 色情報用の量子化テーブルは輝度情報用より歪み量を多く与えます。
★　圧縮率を高めるためには、各周波数成分に思い切った歪みを与えることになります。　 周波数成分の中で直流成分は大切な情報源であるため、あまりカットすことはできないので、 あとは、高次の周波数成分の中から人の目にあまり影響を与えない周波数成分をカットしていくことになります。
★　直流成分を大きくカットすれば圧縮効果はあっても、特に画像の滑らかな部分で歪みが目立ってくるし、 一方、高周波成分を思い切ってカットすれば、 画像の変化の激しい部分で何となくザラツキのある歪みが目立つようになります。
これは、アナログ的に云えば、高周波成分をカットしたことによって、 そのカットした周波数位置で折り返し歪（エイリアシング）が生じているからです。
（幾何学変換のところでアンチエイリアシングと云う言葉が出ておりましたが、 これはこの歪を除去する意味になります。）
また、同じ量子化を与えても画像の背景によって画質に差が生じてきます。　 したがって、画質にこだわるのであれば圧縮率云々よりも、 量子化を各種試して満足いくところを探すことが必要になります。

次回はもう一つ「折り返し歪み」についての話をした上で、 各周波数の量子化によって画質がどう変わるかを実際例で見ていきます。