|
幾何学変換
 幾何学という言葉だけでいやになりそうですが、要するに物体の今ある位置から別の位置へ移動させるということだけで、
そのために現在位置の座標を基準に別の位置の座標に変換してやろうということです。
幾何学という言葉だけでいやになりそうですが、要するに物体の今ある位置から別の位置へ移動させるということだけで、
そのために現在位置の座標を基準に別の位置の座標に変換してやろうということです。
画像の場合は、これによって拡大、縮小、回転、ミラー反転、デフォルメなどいろんな操作ができます。
写真のような静止画像は平面的であり、二次元の世界だけで話がまとまるため最も簡単な操作で済みます。
写真でも、三次元グラフィックス (3DCG) の中で扱うと、見かけ上は三次元になり、
つまり横軸と縦軸だけに位置していた平面画像が奥行き方向にも座標軸を持つようになり、
操作は二次元より多少複雑になります。
これが3DCGの動画になると今度は時間によって動きを変えるわけだから、
そこには時間軸が入ってきて操作は更に複雑になります。
 幾何学変換という言葉はもうやめて座標変換という言葉にします。
つまり、写真を構成する1画素1画素の現在ある座標位置を、
移動する場所の座標位置に変換すれば新しい位置にその写真が組み立てられる訳です。
幾何学変換という言葉はもうやめて座標変換という言葉にします。
つまり、写真を構成する1画素1画素の現在ある座標位置を、
移動する場所の座標位置に変換すれば新しい位置にその写真が組み立てられる訳です。
逆に云えば、新しい座標系にある1点の画素が、現在座標系のどの位置の画素に相当するかを計算し、
その画素を新しい座標系の画素に移すことになります。
★ そのために一つの変換式があります。 まず下の図を見て下さい。
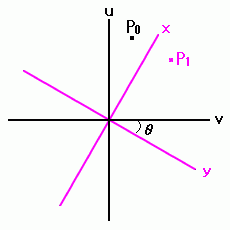 現在位置の座標をU軸、V軸で表し、移動先の座標をX軸、Y軸で表しています。
現在位置の座標をU軸、V軸で表し、移動先の座標をX軸、Y軸で表しています。
この例では、各画素は同じ位置にあって座標軸だけが回転した例を示しており、
UV座標軸がθだけ回転してXY座標軸に変わっています。
これによってUV座標軸からみれば画素P0は、P1へ移動したのと同じになります。
実際の処理では、変換後の新しいXY座標軸の画素P1が変換前のUV座標軸の画素P0にあることを計算によって求め、
これをP1へ移すことになります。
★ 拡大や縮小の場合は、回転角θがゼロで座標軸の長さだけが変わって、
拡大・縮小した座標系へその画素を移動することであり、
したがって、回転も拡大・縮小も同じ考えで処理できます。
★ 次に各画素をどのように移動させるかと云うことですが、これは座標変換として次の式で表現します。
変換前の現在の座標系を (u,v) として、変換後の座標系を (x,y) とすると、
これをマトリックスでは(1)式、方程式では(2)式で表現できます。
通常、これをアフィン変換 (affine transformation) と称して最もよく使われる変換方法です。
これからも分かるように、拡大・縮小、回転、平行移動、ミラー反転などは係数値 (a,b,c,d,e,f) が異なるだけで、
すべてこのアフィン変換に含まれます。 各座標変換によるこれらの係数値は下の表で示しています。
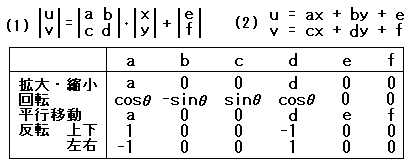
 この表からも分かるように、a,d が拡大率を、e,f が平行移動量を、θが回転量を与えることになります。
この表からも分かるように、a,d が拡大率を、e,f が平行移動量を、θが回転量を与えることになります。
また、a,b,c,d が sinθ、cosθに対応せず、適当な値を代入すると一種のデフォルメ操作になります。
たとえば、a=d=1.0、b=c=-0.5 とすれば、右のような画像に変換されます。
★ 三次元座標系では、上の(1)式で表現すれば、座標軸が (x,y,z) でマトリックスも3X3になり、
複雑にはなるものの理屈は二次元と全く同じことです。
 座標変換は、上の変換式を用いて、
新しい座標軸の各画素位置が変換前の座標軸(原画像)のどの位置に相当するかを求め、
原画像の該当位置の画素値を変換後の画素値とする方法を用いますが、
このとき、変換後の座標位置が原画像のどの整数位置にも対応しなかったり、
誤差によって複数の画素が同じ画素に対応したりして歪が生じるため、
変換後の画素値をいろんな方法で補間処理します。
座標変換は、上の変換式を用いて、
新しい座標軸の各画素位置が変換前の座標軸(原画像)のどの位置に相当するかを求め、
原画像の該当位置の画素値を変換後の画素値とする方法を用いますが、
このとき、変換後の座標位置が原画像のどの整数位置にも対応しなかったり、
誤差によって複数の画素が同じ画素に対応したりして歪が生じるため、
変換後の画素値をいろんな方法で補間処理します。
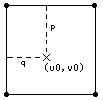 ★ 一般に利用されるのが線形補間で、
これは注目する新しい座標軸上の各位置の画素値は、
対応する原画像の位置の近傍4画素からの距離によって線形補間する方法を用います。
★ 一般に利用されるのが線形補間で、
これは注目する新しい座標軸上の各位置の画素値は、
対応する原画像の位置の近傍4画素からの距離によって線形補間する方法を用います。
もう少し分かりやすく説明すると、
図のように座標変換後の新しい画素位置に対する原画像の画素位置を計算した結果、
画素間のX点 (u0,v0) に該当したとき、
原画像上ではそのような位置が存在しないため、
周囲の4画素からの距離による加重平均で (u0,y0) 位置の画素濃度を求めるのです。
もう少し複雑になると、X点 (u0,v0) の周辺4X4画素から補間する方法を用いることもあります。
 ★ また、これは画像を回転したとき問題になる現象ですが、
回転したことによって原画像の上下、左右の縁にジャギーが生じます。
これも一種の歪みですから、
通常はアンチエイリアシング(不自然さを除く)処理と云う方法でその縁をスムージングして見栄えよくします。
★ また、これは画像を回転したとき問題になる現象ですが、
回転したことによって原画像の上下、左右の縁にジャギーが生じます。
これも一種の歪みですから、
通常はアンチエイリアシング(不自然さを除く)処理と云う方法でその縁をスムージングして見栄えよくします。
この例はジャギーの発生した画像と縁をスムージングした画像の一部を切り出して拡大した例です。
画像を回転したときのこれらの実際例は、
画像処理サンプルのページに掲載しています。
|
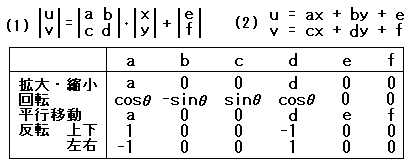
 この表からも分かるように、a,d が拡大率を、e,f が平行移動量を、θが回転量を与えることになります。
この表からも分かるように、a,d が拡大率を、e,f が平行移動量を、θが回転量を与えることになります。 座標変換は、上の変換式を用いて、
新しい座標軸の各画素位置が変換前の座標軸(原画像)のどの位置に相当するかを求め、
原画像の該当位置の画素値を変換後の画素値とする方法を用いますが、
このとき、変換後の座標位置が原画像のどの整数位置にも対応しなかったり、
誤差によって複数の画素が同じ画素に対応したりして歪が生じるため、
変換後の画素値をいろんな方法で補間処理します。
座標変換は、上の変換式を用いて、
新しい座標軸の各画素位置が変換前の座標軸(原画像)のどの位置に相当するかを求め、
原画像の該当位置の画素値を変換後の画素値とする方法を用いますが、
このとき、変換後の座標位置が原画像のどの整数位置にも対応しなかったり、
誤差によって複数の画素が同じ画素に対応したりして歪が生じるため、
変換後の画素値をいろんな方法で補間処理します。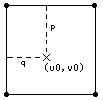 ★ 一般に利用されるのが線形補間で、
これは注目する新しい座標軸上の各位置の画素値は、
対応する原画像の位置の近傍4画素からの距離によって線形補間する方法を用います。
★ 一般に利用されるのが線形補間で、
これは注目する新しい座標軸上の各位置の画素値は、
対応する原画像の位置の近傍4画素からの距離によって線形補間する方法を用います。 ★ また、これは画像を回転したとき問題になる現象ですが、
回転したことによって原画像の上下、左右の縁にジャギーが生じます。
これも一種の歪みですから、
通常はアンチエイリアシング(不自然さを除く)処理と云う方法でその縁をスムージングして見栄えよくします。
★ また、これは画像を回転したとき問題になる現象ですが、
回転したことによって原画像の上下、左右の縁にジャギーが生じます。
これも一種の歪みですから、
通常はアンチエイリアシング(不自然さを除く)処理と云う方法でその縁をスムージングして見栄えよくします。 現在位置の座標をU軸、V軸で表し、移動先の座標をX軸、Y軸で表しています。
現在位置の座標をU軸、V軸で表し、移動先の座標をX軸、Y軸で表しています。