画像を表現するとき、その画像の解像度を上げれば画質も向上しますが、 それよりもその画像を構成する各画素の色表現能力（階調数）がどれだけあるかの方がもっと重要になります。
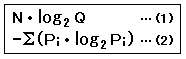一般に画像の情報量は (1)式で表しますが、ここでＮは解像度、Ｑは階調数、LogＱはビット数を示しています。　 ２を底とする対数で表しているのは、デジタル情報の最小単位が０か１の２通りの表現になっているからです。
そして、(2)式は情報理論で云う画像の平均情報量のことでエントロピーと呼ばれています。　 ここでＰiは画素(i)の発生確率を示しています。
ここでいきなり対数で表現してみたのは、これを画像圧縮へつないでいくときの基本になっているからです。
また、エントロピーという言葉も情報を圧縮する（無駄な情報を捨てる）ために欠かせない考え方なっています。
★　ここでは単純に、画像情報は解像度と階調を示すビット数の積で決まるとしておきます。
先ほど、画質を決めるのは解像度より階調数の方が大切だと云いましたが、これは少し違うかも知れません。
と云うことは、画質は最終的には人が見て決める訳ですから、人の視覚特性も考慮せねばならないからです。
これを考慮に入れると、画像の滑らかな部分では解像度より階調の方が大切であり、 変化の激しい部分では逆に階調より解像度の方が大切になります。
このことは効率的な画像圧縮するときの重要な要素になります。
★　もう一つ重要な要素として画像の表示面積があります。
　 何度も出てきましたが、表示面積を小さくしていくと人の目は次第に色や階調の識別能力を失っていき、 最後には黒にしか見えなくなってしまいます。
しかし、ここまで話を広げると複雑になるので、 とりあえずは色の識別能力が十分に満たされる大きさの画像を表示しているとしておきます。

画像の表示面積を固定して解像度や階調数を変えたときの画質がどのように変化するか見てみます。
ＪＰＥＧで高圧縮しているので画質はよくありませんが、右のサンプルを原画像として、 下のサンプルの左側画像は解像度を４分の１に落としてみた例で、 右側画像は各色を４ビット(４Ｘ３色＝１２ビット＝４０９６階調)で表現してみた例です。
この２つの例を比較してみると、画像の中で変化の激しい部分は解像度を落とした左画像の劣化が激しく、 階調を落とした右画像では殆ど劣化が認識できません。　 一方、画像の中で滑らかな部分（背景の空の部分）は解像度を落とした左画像ではあまり劣化が見あたらず、 階調を落とした右画像では擬輪郭が発生しておりかなり劣化していることが分かります。


下の例は解像度を変えないで階調だけを変化させてみた例ですが、 上記のように階調を示すビット数を単純にカットしないで、 画像の局部的な変化に応じて適応的に変化させてみた例です。
左の画像は１６色で表現し、右の画像は２５６色で表現してみた例です。　 何れの画像も変化の激しい部分では劣化はあまり目立ちませんが、 滑らかな部分での劣化が特に左の画像で目立ちます。
★　ところが更にその下のディザ有りの２画像を見てください。　 ここではディザ無し画像に比べて滑らかな部分の劣化が目立たなくなっています。
これはディザによる効果ですが、 ディザ処理は簡単に云えばノイズをばらまくことによって画像を滑らかにしようと云うものであり、 一般によく使われる方法に組織ディザ法と誤差拡散法とありますが、 この仕組みの詳しくは別の機会に掲載します。