３次元グラフィックスの話

page 目に映る現実の姿は３次元空間にありながら、 それを映像として見るときは２次元空間に変換して表示しています。　 写真もビデオも撮った映像は平面上に置かれています。
この平面上で、より現実に近い形で３次元空間を表現するのが３次元グラフィックス（３ＤＣＧ）の世界です。
この３ＤＣＧは写実的な絵画を描くのと作業としては同じようなものですが、 ほとんどが数学の助けを借りて３次元的に描いた物体に光と陰を付けながら絵を生成してみようとするものです。
これを実現するために３ＤＣＧではモデリングとレンダリングという２つの工程を経て絵を生成しますが、 その流れは次のようになっています。

page モデリングは３次元的に描きたい物体のモデルを作る工程で、
(1) 描きたい物体の形を幾何学的に決める形状モデル
(2) その物体の表面の色や材質感を決める表面モデル
(3) 描いた物体を照明する光の性質を決める光源モデル
(4) 物体を見るときの視点の位置や視線の方向、視野角を決める視野モデル
があり、これらは下で述べるいろんな座標系の中に配置されることになります。
また、これらのモデルはコンピュータで扱えるように抽象化したデータとして構成されていなければなりません。

page 下の例は(1)立方体、(2)(3)球体（楕円面）、(4)楕円錐面、(5)二葉双曲面、(6)一葉双曲面、を描いていろんな視点から見た例です。　 この一つ一つの物体が形状モデルであり、同じ物体を視点を変えて見るのが視野モデルになります。
何れも簡単な例ですが、実際の３ＤＣＧではこのような単純な形状モデルを組み合わせて実際に合った複雑な形状モデルを形成していきます。
プリミティブな形状モデルにはこの他に、楕円放物面、２次柱面、楕円柱面、 双曲柱面、放物柱面、自由曲面などがあります。

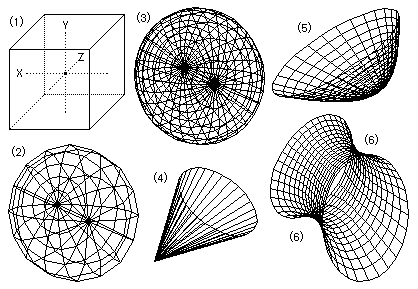
形状モデルpage
たとえば、建物で室内をモデリングしようとすれば、室内自体、柱、床などはほとんど立方体の形状モデルで間に合うでしょうが、 そこに螺旋階段のようなものを入れようとすれば、曲面をもつ形状モデルも必要になってくるでしょう。
★　ここで一つの形状モデルを見て下さい。　すべてがワイヤーフレームで描かれています。　 各線で囲まれた多角形の閉領域をポリゴンと呼んでいますが、 透視図で描かれており本来裏に隠れるはずの線分まで表示しているため、この状態では立体感がはききりとは掴めません。
★　また、同じ球体でも(2)では球体を描く線数が少なく各ポリゴン表面に色を塗ったとき、 ポリゴンの形状跡が映し出されてしまって滑らかな球体にはなりません。　 これに対して(3)のように描画線数を倍にしてみるとかなり滑らかになっています。　 その分ポリゴンの数も球体では４倍になりその処理も４倍多くかかるようになります。
★　このような形状モデルの各ポリゴン表面に色を塗っていくのが別の項で述べるレンダリングですが、 どんな色を塗るかは表面モデルや光源モデルで決まってきます。

page ３次元空間の中で画像を扱っていくわけですから、 その中にある物体や光源、視点の位置、物体の形状などは３次元空間の座標系の中に配置しなければなりません。
このために次のような座標系があります。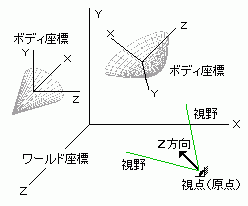
座標系 ・ボディ座標系：独立した個々の物体自身の座標であり、 各物体はこの座標の中で拡大縮小、回転、移動などを行なって目的の形状まで変形することになります。
・ワールド座標系：ボディ座標系の中で描いた個々の物体を配置する座標であり、 この系で座標変換するとその中に配置された物体はすべてが座標変換されることになります。
・視点座標系：ワールド座標系に配置された物体を見るための座標であり、 ワールド座標系に対して視点の位置を原点として視線の方向をＺ軸（奥行き）方向として定めます。
このとき、視点の位置や視線の方向が常に同じであればワールド座標系は視点座標系と同じになるので、 ボディ座標系から直接視点座標系へ変換することができます。　 そしてこの座標系で視点の位置を移動すればワールド座標系の中にある各物体はすべて座標変換されることになります。
・スクリーン座標：視点座標系に置かれた物体を今度はＣＲＴモニターのような平面上に投影して見るために透視変換しますが、 ここではじめてＺ軸がＸＹ平面軸上に変換されるため個々の物体は遠近感をもって表示されるようになります。
そしてスクリーン座標上では、視野からはみ出した部分はクリッピングという手段でカットしてやる必要があります。
★　上図で視点の位置を動かせば、ワールド座標系に配置されている各物体の見え方が変わってきますが、 この場合、視点の位置を動かさないでワールド座標系を回転、拡大縮小などの座標変換しても同じことになります。　 ワールド座標系を変換すればそれに伴ってボディ座標系も変換され、物体の位置も変わってくることになります。

− 2000.1.8. −